Câu hỏi:

28/06/2022 540

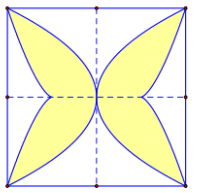
Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp nhất trong toán học. Ở đó có mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ Oxy là \[16{y^2} = {x^2}(25 - {x^2})\;\]như hình vẽ bên. Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ Oxy tương ứng với chiều dài 1 mét

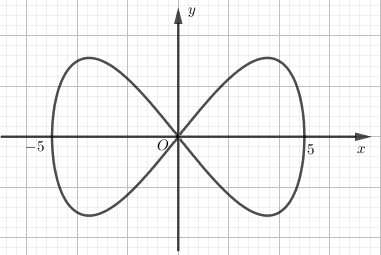
Hoành độ giao điểm của đồ thị với trục hoành là\[x = 0;x = 5;x = - 5\]

Ta thấy diện tích mảnh đất Bernoulli bao gồm diện tích 44 mảnh đất nhỏ bằng nhau.

Xét diện tích S mảnh đất nhỏ trong góc phần tư thứ nhất ta có

\[\begin{array}{*{20}{l}}{4y = x\sqrt {25 - {x^2}} ;x \in \left[ {0;5} \right]}\\{ \Rightarrow S = \frac{1}{4}\mathop \smallint \limits_0^5 x\sqrt {25 - {x^2}} d{\rm{x}} = \frac{{125}}{{12}}}\\{ \Rightarrow S = 4.\frac{{125}}{{12}} = \frac{{125}}{3}\left( {{m^2}} \right)}\end{array}\]

A.\[S = \frac{{125}}{6}({m^2})\]

B. \[S = \frac{{125}}{4}\left( {{m^2}} \right)\]

C. \[S = \frac{{250}}{3}\left( {{m^2}} \right)\]

D. \[S = \frac{{125}}{3}\left( {{m^2}} \right)\]Trả lời:

Xem lời giải

Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Ứng dụng tích phân để tính diện tích !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình \[4{x^2} = {y^4}\;\] và \[4{(|x| - 1)^3} = {y^2}\;\] để tạo hoa văn cho viên gạch. Diện tích phần được tô đậm gần nhất với giá trị nào dưới đây?

A.\[506\,\,\left( {c{m^2}} \right)\]

B. \[747\,\,\left( {c{m^2}} \right)\]

C. \[507\,\,\left( {c{m^2}} \right)\]

D. \[746\,\,\left( {c{m^2}} \right)\]

Lời giải

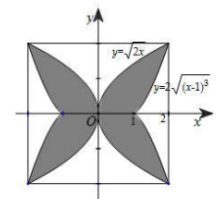
Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình (ảnh 2)

Gắn hệ trục tọa độ như hình vẽ.

Diện tích phần tô đậm là

\[S = 4\left[ {\mathop \smallint \limits_0^1 \left( {\sqrt {2x} - 0} \right)dx + \mathop \smallint \limits_1^2 \left( {\sqrt {2x} - 2\sqrt {{{\left( {x - 1} \right)}^3}} } \right)dx} \right] = \frac{{112}}{{15}}\,\,\left( {d{m^2}} \right) \approx 747\,\,\left( {c{m^2}} \right)\]

Đáp án cần chọn là: B

Câu 2

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S₁ và S₂ (tham khảo hình vẽ).

Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng:

A.\(\frac{1}{2}\)

B. \[\frac{3}{5}\]

C. \[\frac{2}{5}\]

D. \[\frac{1}{3}\]

Lời giải

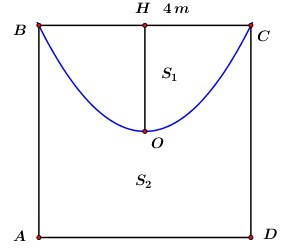
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ). (ảnh 2)

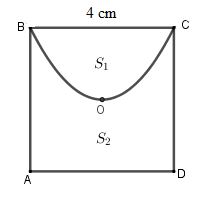
Gọi H là trung điểm của BC.

\[\begin{array}{*{20}{l}}{{S_1} = \frac{4}{3}Rh = \frac{4}{3}.HC.OH = \frac{4}{3}.2.2 = \frac{{16}}{3}\,{m^2}.}\\{{S_{ABCD}} = {4^2} = 16}\\{ \Rightarrow {S_2} = {S_{ABCD}} - {S_1} = 16 - \frac{{16}}{3} = \frac{{32}}{3}\,\,{m^2}.}\\{ \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \frac{{16}}{3}:\frac{{32}}{3} = \frac{1}{2}.}\end{array}\]

Đáp án cần chọn là: A

Câu 3

Cho hai hàm số \[f\left( x \right) = m{x^3} + n{x^2} + px - \frac{5}{2}\left( {m,n,p \in \mathbb{R}} \right)\]và\(g\left( x \right) = {x^2} + 3x - 1\) có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3;−1;1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng

A.\[\frac{9}{2}\]

B.\[\frac{{18}}{5}\]

C.4

D.5

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi

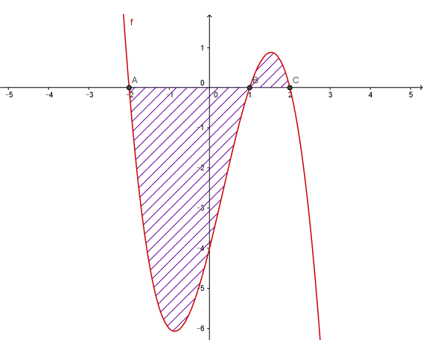
A.\[S = \mathop \smallint \nolimits_{ - 2}^2 f(x)dx\]

B. \[S = \mathop \smallint \nolimits_1^{ - 2} f(x)dx + \mathop \smallint \nolimits_1^2 f(x)dx\]

C. \[S = \mathop \smallint \nolimits_{ - 2}^1 f(x)dx + \mathop \smallint \nolimits_1^2 f(x)dx\]

D. \[S = \mathop \smallint \nolimits_{ - 2}^1 f(x)dx - \mathop \smallint \nolimits_1^2 f(x)dx\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tính diện tích hình phẳng giới hạn bởi hai đường: \[y = \left| {{x^2} - 4x + 3} \right|\,\,\,;\,\,y = x + 3\]

A.\[\frac{{107}}{6}\]

B. \[\frac{{109}}{6}\]

C. \[\frac{{109}}{7}\]

D. \[\frac{{109}}{8}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \[y = {x^3} - x;y = 2x\] và các đường thẳng \[x = - 1;x = 1\;\] được xác định bởi công thức:

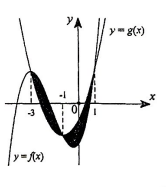
A.\[S = \left| {\mathop \smallint \nolimits_{ - 1}^1 \left( {3x - {x^3}} \right)dx} \right|\]

B. \[S = \mathop \smallint \nolimits_{ - 1}^0 \left( {3x - {x^3}} \right)dx + \mathop \smallint \nolimits_0^1 \left( {{x^3} - 3x} \right)dx\]

C. \[S = \mathop \smallint \nolimits_{ - 1}^1 \left( {3x - {x^3}} \right)dx\]

D. \[S = \mathop \smallint \nolimits_{ - 1}^0 \left( {{x^3} - 3x} \right)dx + \mathop \smallint \nolimits_0^1 \left( {3x - {x^3}} \right)dx\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số \[y = {x^2} - 4\;\] và \[y = x - 4\]

A.\[S = \frac{{16}}{3}\]

B. \[S = \frac{{161}}{6}\]

C. \[S = \frac{1}{6}\]

D. \[S = \frac{5}{6}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ). Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng:

Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi

Tính diện tích hình phẳng giới hạn bởi hai đường: \[y = \left| {{x^2} - 4x + 3} \right|\,\,\,;\,\,y = x + 3\]

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \[y = {x^3} - x;y = 2x\] và các đường thẳng \[x = - 1;x = 1\;\] được xác định bởi công thức:

Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số \[y = {x^2} - 4\;\] và \[y = x - 4\]

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S₁ và S₂ (tham khảo hình vẽ).

Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng: