ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Ứng dụng tích phân để tính diện tích
71 người thi tuần này 4.6 2.1 K lượt thi 27 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
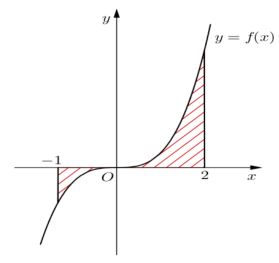
Câu 1
A. \[S = \mathop \smallint \limits_a^b f\left( x \right)dx\]
B. \[S = \mathop \smallint \limits_0^b f\left( x \right)dx\]
C. \[S = \mathop \smallint \limits_b^a \left| {f\left( x \right)} \right|dx\]
D. \[S = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\]
Lời giải
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số\[y = f\left( x \right)\] đường thẳng y=0 và hai đường thẳng\[x = a,x = b\] là\[S = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\]
Đáp án cần chọn là: D
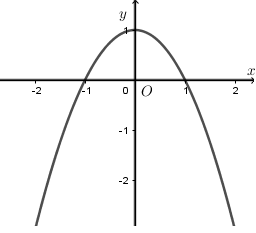
Câu 2
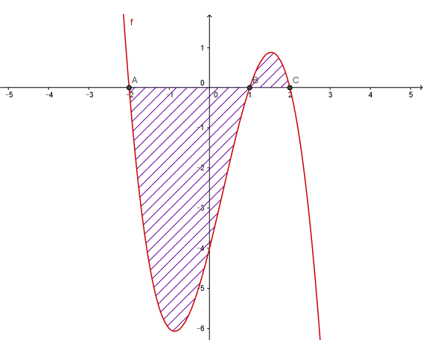
A.\[S = \mathop \smallint \limits_{ - 3}^{ - 1} \left| {{x^2} - 1} \right|dx\]
B. \[S = \mathop \smallint \limits_{ - 1}^{ - 3} \left| {{x^2} - 1} \right|dx\]
C. \[S = \mathop \smallint \limits_{ - 3}^0 \left| {{x^2} - 1} \right|dx\]
D. \[S = \mathop \smallint \limits_{ - 3}^{ - 1} \left( {1 - {x^2}} \right)dx\]
Lời giải
Đáp án cần chọn là: A
Câu 3
A.\[S = \mathop \smallint \limits_a^b \left( {f\left( x \right) - g\left( x \right)} \right)dx\]
B. \[S = \mathop \smallint \limits_a^b \left( {g\left( x \right) - f\left( x \right)} \right)dx\]
C. \[S = \mathop \smallint \limits_a^b \left| {f\left( x \right) - g\left( x \right)} \right|dx\]
D. \[S = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx - \mathop \smallint \limits_a^b \left| {g\left( x \right)} \right|dx\]
Lời giải
Đáp án cần chọn là: C
Câu 4
A.\[S = \mathop \smallint \limits_0^e \left| {{e^x} + x} \right|dx\]
B. \[S = \mathop \smallint \limits_0^e \left| {{e^x} - x} \right|dx\]
C. \[S = \mathop \smallint \limits_e^0 \left| {{e^x} - x} \right|dx\]
D. \[S = \mathop \smallint \limits_e^0 \left| {{e^x} + x} \right|dx\]
Lời giải
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số\[y = f\left( x \right),y = g\left( x \right)\] và hai đường thẳng \[x = 0,x = e\] là:
\[S = \mathop \smallint \limits_0^e \left| {{e^x} - \left( { - x} \right)} \right|dx = \mathop \smallint \limits_0^e \left| {{e^x} + x} \right|dx\]
Đáp án cần chọn là: A
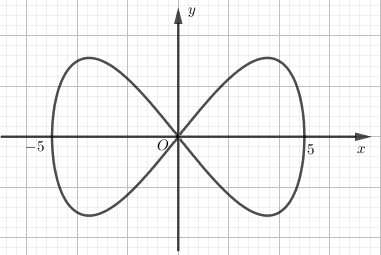
Câu 5
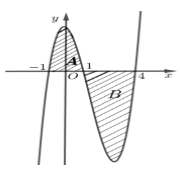
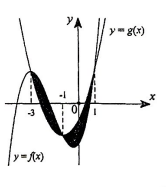
A.\[S = \left| {\mathop \smallint \nolimits_{ - 1}^1 \left( {3x - {x^3}} \right)dx} \right|\]
B. \[S = \mathop \smallint \nolimits_{ - 1}^0 \left( {3x - {x^3}} \right)dx + \mathop \smallint \nolimits_0^1 \left( {{x^3} - 3x} \right)dx\]
C. \[S = \mathop \smallint \nolimits_{ - 1}^1 \left( {3x - {x^3}} \right)dx\]
D. \[S = \mathop \smallint \nolimits_{ - 1}^0 \left( {{x^3} - 3x} \right)dx + \mathop \smallint \nolimits_0^1 \left( {3x - {x^3}} \right)dx\]
Lời giải
Xét phương trình hoành độ giao điểm của 2 đồ thị:
\[{x^3} - x = 2x \Leftrightarrow {x^3} - 3x = 0 \Leftrightarrow x = 0\] (chỉ xét trên\[\left( { - 1;1} \right)\]
Với\[x \in \left( { - 1;0} \right)\] thì\[{x^3} - 3x > 0\] với \[x \in \left( {0;1} \right)\] thì \[{x^3} - 3x < 0\]
Diện tích cần tìm là \[S = \mathop \smallint \limits_{ - 1}^1 \left| {{x^3} - 3x} \right|dx = \mathop \smallint \limits_{ - 1}^0 \left( {{x^3} - 3x} \right)dx + \mathop \smallint \limits_0^1 \left( {3x - {x^3}} \right)dx\]
Đáp án cần chọn là: D
Câu 6
A.\[S = 2 + e\]
B. \[S = 2 - e\]
C. \[S = e - 2\]
D. \[S = e - 1\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[S = b - a.\]
B. \[S = b + a.\]
C. \[S = - b + a.\]
D. \[S = - b - a.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A.\[S = \frac{{16}}{3}\]
B. \[S = \frac{{161}}{6}\]
C. \[S = \frac{1}{6}\]
D. \[S = \frac{5}{6}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A.\[\pi + \frac{4}{3}\]
B. \[\frac{\pi }{2} - 1\]
C. \[\frac{\pi }{2}\]
D. \[\frac{\pi }{2} + \frac{1}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
B. \[S = \left| {\mathop \smallint \limits_0^2 \left( {{x^3} + x - 2} \right)d{\rm{x}}} \right|\]
C. \[S = \frac{1}{2} + \mathop \smallint \limits_0^1 {x^3}d{\rm{x}}\]
D. \[S = \mathop \smallint \limits_0^1 \left| {{x^3} + x - 2} \right|d{\rm{x}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A.\[S = \mathop \smallint \limits_{ - 1}^0 f(x)dx + \mathop \smallint \limits_0^1 |f(x)|dx\]
B. \[\mathop \smallint \limits_{ - 1}^1 \left| {f\left( x \right)} \right|dx\]
C. \[S = \mathop \smallint \limits_{ - 1}^1 f(x)dx\]
D. \[S = \left| {\mathop \smallint \limits_{ - 1}^1 f(x)dx} \right|\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A.\[S = \frac{{125}}{6}({m^2})\]
B. \[S = \frac{{125}}{4}\left( {{m^2}} \right)\]
C. \[S = \frac{{250}}{3}\left( {{m^2}} \right)\]
D. \[S = \frac{{125}}{3}\left( {{m^2}} \right)\]Trả lời:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A.\[\frac{{107}}{6}\]
B. \[\frac{{109}}{6}\]
C. \[\frac{{109}}{7}\]
D. \[\frac{{109}}{8}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A.0 .
B.16
C.4 .
D.8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A.\[S = \frac{8}{3}\]
B. \[S = 1\]
C. \[S = \frac{4}{3}\]
D. \[S = 2\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
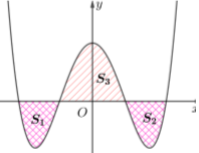
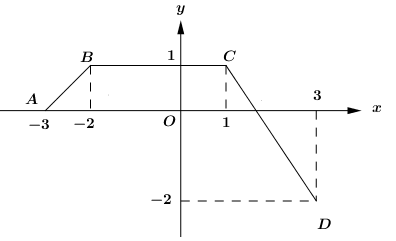
A.\[S = \mathop \smallint \nolimits_{ - 2}^2 f(x)dx\]
B. \[S = \mathop \smallint \nolimits_1^{ - 2} f(x)dx + \mathop \smallint \nolimits_1^2 f(x)dx\]
C. \[S = \mathop \smallint \nolimits_{ - 2}^1 f(x)dx + \mathop \smallint \nolimits_1^2 f(x)dx\]
D. \[S = \mathop \smallint \nolimits_{ - 2}^1 f(x)dx - \mathop \smallint \nolimits_1^2 f(x)dx\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A.\[\frac{{128}}{3}{m^2}\]
B. \[\frac{{131}}{3}{m^2}\]
C. \[\frac{{28}}{3}{m^2}\]
D. \[\frac{{26}}{3}m\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A.\[S = \frac{8}{3}\]
B. \[S = \frac{4}{3}\]
C. \[S = 4\]
D. \[S = \frac{{16}}{9}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A.\[\frac{{253}}{{12}}\]
B. \[\frac{{253}}{{24}}\]
C. \[ - \frac{{125}}{{24}}\]
D. \[ - \frac{{125}}{{12}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A.\[506\,\,\left( {c{m^2}} \right)\]
B. \[747\,\,\left( {c{m^2}} \right)\]
C. \[507\,\,\left( {c{m^2}} \right)\]
D. \[746\,\,\left( {c{m^2}} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A.\(\frac{1}{2}\)
B. \[\frac{3}{5}\]
C. \[\frac{2}{5}\]
D. \[\frac{1}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A.\[\frac{5}{2}\]
B. \[\frac{{35}}{6}\]
C. \[\frac{{ - 5}}{2}\]
D. \[\frac{{ - 35}}{6}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A.1.954.000 đồng
B.2.123.000 đồng
C.1.946.000 đồng
D.2.145.000 đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A.\[\frac{9}{2}\]
B.\[\frac{{18}}{5}\]
C.4
D.5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A.2ln3.
B.ln3.
C.ln18.
D.2ln2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.