Câu hỏi:

28/06/2022 287

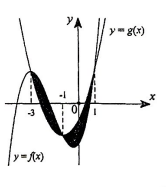
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.

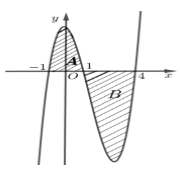
Diện tích hai phần A và B lần lượt là \(\frac{{16}}{3}\) và \(\frac{{63}}{4}\). Tính \[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx\]

A.\[\frac{{253}}{{12}}\]

B. \[\frac{{253}}{{24}}\]

C. \[ - \frac{{125}}{{24}}\]

D. \[ - \frac{{125}}{{12}}\]

Xem lời giải

Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Ứng dụng tích phân để tính diện tích !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Xét \[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx\] Đặt\[2x + 1 = t \Leftrightarrow 2dx = dt \Leftrightarrow dx = \frac{{dt}}{2}\]

Đổi cận:\(\left\{ {\begin{array}{*{20}{c}}{x = - 1 \Rightarrow t = - 1}\\{x = \frac{3}{2} \Rightarrow t = 4}\end{array}} \right.\)

Khi đó ta có\[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx = \frac{1}{2}\mathop \smallint \limits_{ - 1}^4 f\left( t \right)dt = \frac{1}{2}\mathop \smallint \limits_{ - 1}^4 f\left( x \right)dx\]

\[ = \frac{1}{2}\left( {\mathop \smallint \limits_{ - 1}^1 f\left( x \right)dx + \mathop \smallint \limits_1^4 f\left( x \right)dx} \right)\]

Từ hình vẽ ta có\[\mathop \smallint \limits_{ - 1}^1 f\left( x \right)dx = \frac{{16}}{3};\,\mathop \smallint \limits_1^4 f\left( x \right)dx = - \frac{{63}}{4}\]

Nên\[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx = \frac{1}{2}\left( {\mathop \smallint \limits_{ - 1}^1 f\left( x \right)dx + \mathop \smallint \limits_1^4 f\left( x \right)dx} \right) = \frac{1}{2}\left( {\frac{{16}}{3} - \frac{{63}}{4}} \right) = - \frac{{125}}{{24}}\]

Đáp án cần chọn là: C

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình \[4{x^2} = {y^4}\;\] và \[4{(|x| - 1)^3} = {y^2}\;\] để tạo hoa văn cho viên gạch. Diện tích phần được tô đậm gần nhất với giá trị nào dưới đây?

A.\[506\,\,\left( {c{m^2}} \right)\]

B. \[747\,\,\left( {c{m^2}} \right)\]

C. \[507\,\,\left( {c{m^2}} \right)\]

D. \[746\,\,\left( {c{m^2}} \right)\]

Lời giải

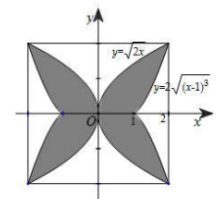
Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình (ảnh 2)

Gắn hệ trục tọa độ như hình vẽ.

Diện tích phần tô đậm là

\[S = 4\left[ {\mathop \smallint \limits_0^1 \left( {\sqrt {2x} - 0} \right)dx + \mathop \smallint \limits_1^2 \left( {\sqrt {2x} - 2\sqrt {{{\left( {x - 1} \right)}^3}} } \right)dx} \right] = \frac{{112}}{{15}}\,\,\left( {d{m^2}} \right) \approx 747\,\,\left( {c{m^2}} \right)\]

Đáp án cần chọn là: B

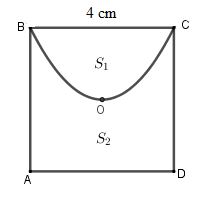
Câu 2

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S₁ và S₂ (tham khảo hình vẽ).

Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng:

A.\(\frac{1}{2}\)

B. \[\frac{3}{5}\]

C. \[\frac{2}{5}\]

D. \[\frac{1}{3}\]

Lời giải

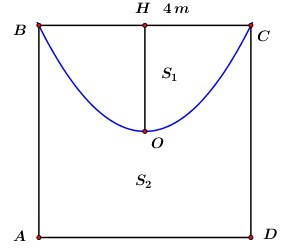
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ). (ảnh 2)

Gọi H là trung điểm của BC.

\[\begin{array}{*{20}{l}}{{S_1} = \frac{4}{3}Rh = \frac{4}{3}.HC.OH = \frac{4}{3}.2.2 = \frac{{16}}{3}\,{m^2}.}\\{{S_{ABCD}} = {4^2} = 16}\\{ \Rightarrow {S_2} = {S_{ABCD}} - {S_1} = 16 - \frac{{16}}{3} = \frac{{32}}{3}\,\,{m^2}.}\\{ \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \frac{{16}}{3}:\frac{{32}}{3} = \frac{1}{2}.}\end{array}\]

Đáp án cần chọn là: A

Câu 3

Cho hai hàm số \[f\left( x \right) = m{x^3} + n{x^2} + px - \frac{5}{2}\left( {m,n,p \in \mathbb{R}} \right)\]và\(g\left( x \right) = {x^2} + 3x - 1\) có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3;−1;1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng

A.\[\frac{9}{2}\]

B.\[\frac{{18}}{5}\]

C.4

D.5

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi

A.\[S = \mathop \smallint \nolimits_{ - 2}^2 f(x)dx\]

B. \[S = \mathop \smallint \nolimits_1^{ - 2} f(x)dx + \mathop \smallint \nolimits_1^2 f(x)dx\]

C. \[S = \mathop \smallint \nolimits_{ - 2}^1 f(x)dx + \mathop \smallint \nolimits_1^2 f(x)dx\]

D. \[S = \mathop \smallint \nolimits_{ - 2}^1 f(x)dx - \mathop \smallint \nolimits_1^2 f(x)dx\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tính diện tích hình phẳng giới hạn bởi hai đường: \[y = \left| {{x^2} - 4x + 3} \right|\,\,\,;\,\,y = x + 3\]

A.\[\frac{{107}}{6}\]

B. \[\frac{{109}}{6}\]

C. \[\frac{{109}}{7}\]

D. \[\frac{{109}}{8}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \[y = {x^3} - x;y = 2x\] và các đường thẳng \[x = - 1;x = 1\;\] được xác định bởi công thức:

A.\[S = \left| {\mathop \smallint \nolimits_{ - 1}^1 \left( {3x - {x^3}} \right)dx} \right|\]

B. \[S = \mathop \smallint \nolimits_{ - 1}^0 \left( {3x - {x^3}} \right)dx + \mathop \smallint \nolimits_0^1 \left( {{x^3} - 3x} \right)dx\]

C. \[S = \mathop \smallint \nolimits_{ - 1}^1 \left( {3x - {x^3}} \right)dx\]

D. \[S = \mathop \smallint \nolimits_{ - 1}^0 \left( {{x^3} - 3x} \right)dx + \mathop \smallint \nolimits_0^1 \left( {3x - {x^3}} \right)dx\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hai hàm số \[f(x) = - x\;\] và \[g(x) = {e^x}\]. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \[y = f(x),y = g(x)\;\] và hai đường thẳng x=0,x=e là:

A.\[S = \mathop \smallint \limits_0^e \left| {{e^x} + x} \right|dx\]

B. \[S = \mathop \smallint \limits_0^e \left| {{e^x} - x} \right|dx\]

C. \[S = \mathop \smallint \limits_e^0 \left| {{e^x} - x} \right|dx\]

D. \[S = \mathop \smallint \limits_e^0 \left| {{e^x} + x} \right|dx\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Diện tích hai phần A và B lần lượt là \(\frac{{16}}{3}\) và \(\frac{{63}}{4}\). Tính \[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx\]

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ). Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng:

Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi

Tính diện tích hình phẳng giới hạn bởi hai đường: \[y = \left| {{x^2} - 4x + 3} \right|\,\,\,;\,\,y = x + 3\]

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \[y = {x^3} - x;y = 2x\] và các đường thẳng \[x = - 1;x = 1\;\] được xác định bởi công thức:

Cho hai hàm số \[f(x) = - x\;\] và \[g(x) = {e^x}\]. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \[y = f(x),y = g(x)\;\] và hai đường thẳng x=0,x=e là:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.

Diện tích hai phần A và B lần lượt là \(\frac{{16}}{3}\) và \(\frac{{63}}{4}\). Tính \[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx\]

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S₁ và S₂ (tham khảo hình vẽ).

Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng: