Cho số phức z thỏa mãn \[\left| {z - 2 - 2i} \right| = 1\]. Số phức z−i có mô đun nhỏ nhất là:
A.\[\sqrt 5 - 1\]
B. \[1 - \sqrt 5 \]
C. \[\sqrt 5 + 1\]
D. \[\sqrt 5 + 2\]
Quảng cáo
Trả lời:
Ta có:
\[\left| {z - i} \right| = \left| {\left( {z - 2 - 2i} \right) + \left( {i + 2} \right)} \right| \ge \left| {\left| {z - 2 - 2i} \right| - \left| {i + 2} \right|} \right| = \left| {1 - \sqrt 5 } \right| = \sqrt 5 - 1\]
Vậy\[\left| {z - i} \right| \ge \sqrt 5 - 1\]nên\[\min \left| {z - i} \right| = \sqrt 5 - 1\]
Đáp án cần chọn là: A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo bất đẳng thức chứa dấu giá trị tuyệt đối ta có
\[|z + 2 + i| = |(z - 1 - 2i) + (3 + 3i)| \ge ||z - 1 - 2i| - |3 + 3i|| = |4 - 3\sqrt 2 | = 3\sqrt 2 - 4 = m\]
\[|z + 2 + i| = |(z - 1 - 2i) + (3 + 3i)| \le |z - 1 - 2i| + |3 + 3i| = 4 + 3\sqrt 2 = M\]
Suy ra
\[{M^2} + {m^2} = {(3\sqrt 2 - 4)^2} + {(4 + 3\sqrt 2 )^2} = 2({4^2} + {(3\sqrt 2 )^2}) = 68\]
Đáp án cần chọn là: C
Câu 2
A.\[\frac{{\sqrt {221} }}{5}.\]
B. \[\sqrt 5 \]
C. 3
D. \[\frac{{\sqrt {29} }}{5}\]
Lời giải
Cách 1: Dùng phương pháp hình học →→ Kỹ năng dồn số phức.
\[P = \left| {z + i\,{\rm{\bar w}} - 6 - 8i} \right| = \left| {\left( {z - 6 - 8i} \right) - \left( { - i\bar w} \right)} \right| = \left| {u - v} \right|\]
Trong đó:\(\left\{ {\begin{array}{*{20}{c}}{u = z - 6 - 8i}\\{v = - i\overline {\rm{w}} }\end{array}} \right.\) u có điểm biểu diễn là A, v có điểm biểu diễn là B.
\[ \Rightarrow P = \left| {u - v} \right| = AB \Rightarrow \]Cần đạt Min.
\[\left| z \right| = 1 \Leftrightarrow \left| {\left( {z - 6 - 8i} \right) + 6 + 8i} \right| = 1 \Leftrightarrow \left| {u + 6 + 8i} \right| = 1\]
⇒ Tập hợp điểm A biểu diễn số phức uu là đường tròn: \[\left( {{C_1}} \right):\left\{ {\begin{array}{*{20}{c}}{I( - 6; - 8)}\\{{R_1} = 1}\end{array}} \right.\]
\[\left| w \right| = 2 \Leftrightarrow \left| {\bar w} \right| = 2 \Leftrightarrow \left| { - i} \right|.\left| {\bar w} \right| = \left| { - i} \right|.2 \Rightarrow \left| { - i\bar w} \right| = 2 \Leftrightarrow \left| v \right| = 2\]
⇒ Tập hợp điểm B biểu diễn số phức v là đường tròn\[\;({C_2}):\left\{ {\begin{array}{*{20}{c}}{O(0;0)}\\{{R_2} = 2}\end{array}} \right.\]
Có\(\left\{ {\begin{array}{*{20}{c}}{IA = {R_1} = 1}\\{OB = {R_2} = 2}\\{OI = 10}\end{array}} \right.\)
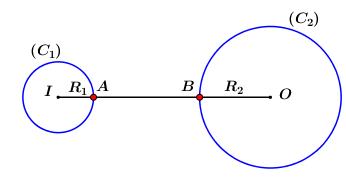
\[ \Rightarrow A{B_{\min }} = IO - {R_1} - {R_2} = 10 - 1 - 2 = 7\]
Min đạt được khi:\(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {OA} = \frac{9}{{10}}\overrightarrow {OI} \Rightarrow A\left( {\frac{{ - 27}}{5};\frac{{ - 36}}{5}} \right) \Rightarrow u = - \frac{{27}}{5} - \frac{{36}}{5}i}\\{\overrightarrow {OB} = \frac{1}{5}\overrightarrow {OI} \Rightarrow B\left( {\frac{{ - 6}}{5};\frac{{ - 8}}{5}} \right) \Rightarrow v = - \frac{6}{5} - \frac{8}{5}i}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{z = u + 6 + 8i = \frac{3}{5} + \frac{4}{5}i}\\{ - i\overline {\rm{w}} = v \Rightarrow \overline {\rm{w}} = \frac{v}{{ - i}} = \frac{{ - \frac{6}{5} - \frac{8}{5}i}}{{ - i + \frac{6}{5}i}} = \frac{8}{5} - \frac{6}{5}i \Rightarrow {\rm{w}} = \frac{8}{5}}\end{array}} \right.\)
\[ \Rightarrow \left| {z - w} \right| = \left| {\left( {\frac{3}{5} + \frac{4}{5}i} \right) - \left( {\frac{8}{5} + \frac{6}{5}i} \right)} \right| = \frac{{\sqrt {29} }}{5}\]
Cách 2: Phương pháp dùng BĐT vectơ
Ta có BĐT cho 3 vectơ\[\vec a,\,\,\vec b,\,\,\vec c\]thì\[\left| {\vec a + \vec b + \vec c} \right| \ge \left| {\vec a} \right| - \left| {\vec b} \right| - \left| {\vec c} \right|\]
Dấu “=” xảy ra ⇔\(\left\{ {\begin{array}{*{20}{c}}{\left| {\overrightarrow a } \right| \ge \left| {\overrightarrow b } \right| + \left| {\overrightarrow c } \right|}\\{\overrightarrow a = k\overrightarrow b }\\{\overrightarrow a = m\overrightarrow c }\end{array}} \right.(k;m < 0)\)
* Đặt\[P = \left| {z + i\,{\rm{\bar w}} - 6 - 8i} \right| = \left| {\underbrace {\left( { - 6 - 8i} \right)}_{ = \overrightarrow a } + \underbrace z_{ = \overrightarrow b } + \underbrace {i\overline {\rm{w}} }_{ = \overrightarrow c }} \right|\]
Đặt\(\left\{ {\begin{array}{*{20}{c}}{( - 6 - 8i) \Leftrightarrow \overrightarrow a ( - 6; - 8) \Rightarrow \left| {\overrightarrow a } \right| = 10}\\{z \Leftrightarrow \overrightarrow b \Rightarrow \left| {\overrightarrow b } \right| = 1}\\{i\overline {\rm{w}} \Leftrightarrow \overrightarrow c \Rightarrow \left| {\overrightarrow c } \right| = \left| {i\overline {\rm{w}} } \right| = \left| {\rm{w}} \right| = 2}\end{array}} \right.\)
\[ \Rightarrow P = \left| {\vec a + \vec b + \vec c} \right| \ge \left| {\vec a} \right| - \left| {\vec b} \right| - \left| {\vec c} \right| = 10 - 1 - 2 = 7\]
\[ \Rightarrow {P_{\min }} = 7\]đạt Min khi\(\left\{ {\begin{array}{*{20}{c}}{\left| {\overrightarrow a } \right| \ge \left| {\overrightarrow b } \right| + \left| {\overrightarrow c } \right|(dung\,do10 > 1 + 2)}\\{\overrightarrow a = - 10\overrightarrow b \Leftrightarrow \overrightarrow b = - \frac{1}{{10}}\overrightarrow a = \left( {\frac{3}{5};\frac{4}{5}} \right)}\\{\overrightarrow a = - 5\overrightarrow c \Leftrightarrow \overrightarrow c = - \frac{1}{5}\overrightarrow a = \left( {\frac{6}{5};\frac{8}{5}} \right)}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{z = \frac{3}{5} + \frac{4}{5}i}\\{i\overline {\rm{w}} = \frac{6}{5} + \frac{8}{5}i \Leftrightarrow {\rm{w}} = \frac{8}{5} + \frac{6}{5}i}\end{array}} \right.\)
\[ \Rightarrow \left| {z - w} \right| = \left| {\left( {\frac{3}{5} + \frac{4}{5}i} \right) - \left( {\frac{8}{5} + \frac{6}{5}i} \right)} \right| = \frac{{\sqrt {29} }}{5}\]
Đáp án cần chọn là: D
Câu 3
A.\[16 + \sqrt {74} \]
B. \[2 + \sqrt {130} \]
C. \[4 + \sqrt {74} \]
D. \[4 + \sqrt {130} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[\left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|\]
B. \[\left| {{z_1} + {z_2}} \right| = \left| {{z_1}} \right| + \left| {{z_2}} \right|\]
C. \[\left| {{z_1} + {z_2}} \right| \ge \left| {{z_1}} \right| + \left| {{z_2}} \right|\]
D. \[\left| {{z_1} + {z_2}} \right| = \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_1} - {z_2}} \right|\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.z=1+i
B.z=3+i
C.z=3+3i
D.z=1+3i
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.2 và 5
B.1 và 6
C.2 và 6
D.1 và 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.