Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD song song với BC, AD=2BC. Gọi E, F là hai điểm lần lượt nằm trên các cạnh AB và AD sao cho \[\frac{{3AB}}{{AE}} + \frac{{AD}}{{AF}} = 5\;\] (E,F không trùng với A), Tổng giá trị lớn nhất và giá trị nhỏ nhất của tỉ số thể tích hai khối chóp S.BCDFE và S.ABCD là:
A.\[\frac{5}{4}\]
B. \[\frac{4}{3}\]
C. \[\frac{{17}}{{12}}\]
D. \[\frac{7}{6}\]
Quảng cáo
Trả lời:
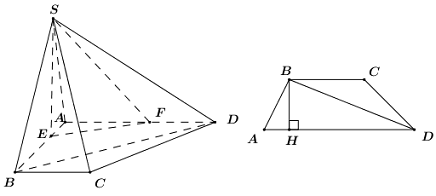
Đặt \[\frac{{AE}}{{AB}} = x,\,\,\frac{{AF}}{{AD}} = y\,\,(0 < x,\,\,y \le 1)\]Theo bài ra ta có\[\frac{{3AB}}{{AE}} + \frac{{AD}}{{AF}} = 5\]
\[ \Rightarrow \frac{3}{x} + \frac{1}{y} = 5\,\,\,\left( 1 \right)\]
Vì hai khối chóp S.BCDFE và S.ABCD có cùng chiều cao nên
\[k = \frac{{{V_{S.BCDFE}}}}{{{V_{S.ABCD}}}} = \frac{{{S_{BCDFE}}}}{{{S_{ABCD}}}}\]
Đặt\[{S_{ABCD}} = S\] kẻ\[BH \bot AD\,\,\left( {H \in AD} \right)\]ta có
\[S = \frac{1}{2}BH.\left( {BC + AD} \right) = \frac{3}{2}.BH.BC\]
Ta có:\[\frac{{{S_{AEF}}}}{{{S_{ABD}}}} = \frac{{\frac{1}{2}AE.AF.\sin \angle BAD}}{{\frac{1}{2}AB.AD.\sin \angle BAD}} = xy \Rightarrow {S_{AEF}} = xy.{S_{ABD}}\]
Mà\[{S_{ABD}} = \frac{1}{2}BH.AD\]nên
\[{S_{AEF}} = \frac{1}{2}xy.BH.AD = xy.BH.BC = \frac{3}{2}BH.BC.\frac{2}{3}xy \Rightarrow {S_{AEF}} = \frac{2}{3}xy.S\]
\[ \Rightarrow {S_{BCDFE}} = {S_{ABCD}} - {S_{AEF}} = S - \frac{2}{3}xy.S = S\left( {1 - \frac{2}{3}xy} \right)\]
\[ \Rightarrow k = \frac{{S.\left( {1 - \frac{2}{3}xy} \right)}}{S} = 1 - \frac{2}{3}xy\]
Theo (1) ta có:\[\frac{3}{x} + \frac{1}{y} = 5 \Leftrightarrow y = \frac{x}{{5x - 3}}\]
Ta có
\[0 < \frac{x}{{5x - 3}} \le 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{x}{{5x - 3}} > 0}\\{\frac{{x - 5x + 3}}{{5x - 3}} \le 0}\end{array}} \right.\]</>
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5x - 3 > 0\,(do\,\,x > 0)}\\{3 - 4x \le 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > \frac{3}{5}}\\{x \ge \frac{3}{4}}\end{array}} \right. \Leftrightarrow x \ge \frac{3}{4}\)
Khi đó ta có
\[\begin{array}{*{20}{l}}{k = 1 - \frac{2}{3}xy = 1 - \frac{2}{3}x.\frac{x}{{5x - 3}}}\\{\,\,\,\, = 1 - \frac{{2{x^2}}}{{3\left( {5x - 3} \right)}} = \frac{{15x - 9 - 2{x^2}}}{{3\left( {5x - 3} \right)}} = f\left( x \right)}\end{array}\]
Xét hàm số\[f\left( x \right) = \frac{{ - 2{x^2} + 15x - 9}}{{3\left( {5x - 3} \right)}}\]với \[\frac{3}{4} \le x \le 1\]ta có:
\[f\prime (x) = {\frac{{( - 4x + 15).3(5x - 3) - ( - 2{x^2} + 15x - 9).15}}{{9{{(5x - 3)}^2}}}^{}}\]
\[f\prime (x) = \frac{{3( - 20{x^2} + 87x - 45) - ( - 30{x^2} + 225x - 135)}}{{9{{(5x - 3)}^2}}}\]
\[f\prime (x) = \frac{{ - 30{x^2} + 36x}}{{9{{(5x - 3)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{6}{5}\left( {ktm} \right)}\\{x = 0\left( {ktm} \right)}\end{array}} \right.\]
BBT:
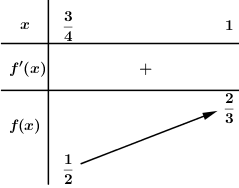
\[ \Rightarrow {k_{\min }} = \frac{1}{2},\,\,{k_{\max }} = \frac{2}{3}\]
Vậy\[{k_{\min }} + {k_{\max }} = \frac{1}{2} + \frac{2}{3} = \frac{7}{6}\]
Đáp án cần chọn là: D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\frac{5}{3}\]
B. \[\frac{2}{3}\]
C. \[\frac{3}{2}\]
D. \[\frac{3}{5}\]
Lời giải
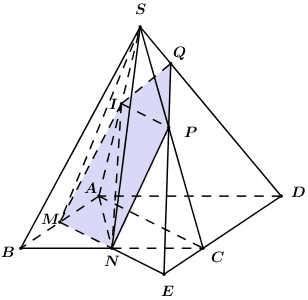
Giả sử\[SC \cap \left( {IMN} \right) = \left\{ P \right\} \Rightarrow \left( {IMN} \right) \cap \left( {SAC} \right) = IP\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{(IMN) \cap (SAC) = IP}\\{(IMN) \cap (ABCD) = MN}\\{(SAC) \cap (ABCD) = AC}\end{array}} \right. \Rightarrow IP\parallel MN\parallel AC\)
Trong (ABCD) gọi \[\left\{ E \right\} = MN \cap CD\]trong (SCD) gọi \[Q = NP \cap SD\]
Khi đó thiết diện của hình chóp cắt bởi (MNI) là ngũ giác IMNPQ.
Gọi\[SM \cap \left( {ABCD} \right) = E \Rightarrow \frac{{d\left( {M;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \frac{{ME}}{{SE}} = \frac{{11}}{{35}}\]theo bài ra ta có\[\frac{{{V_2}}}{{{V_1}}} = \frac{{{V_{M.ACD}}}}{{{V_{S.ABCD}}}} = \frac{{\frac{1}{3}.d\left( {M;\left( {ABCD} \right)} \right).{S_{ACD}}}}{{\frac{1}{3}.d\left( {S;\left( {ABCD} \right)} \right).{S_{ABCD}}}} = \frac{{11}}{{35}}.\frac{1}{2} = \frac{{11}}{{70}}\]
Ta có \[{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\]
Đặt\[\frac{{SI}}{{SA}} = x\,\,\,(0 < x < 1)\]áp dụng định lí Ta-lét ta có\[\frac{{SI}}{{SA}} = \frac{{SP}}{{SC}} = x\]
- Xét khối chóp S.BMN và S.ABCD:
+ Có cùng chiều cao (cùng bằng khoảng cách từ SS đến (ABCD).
\[{S_{BMN}} = \frac{1}{4}{S_{ABC}} = \frac{1}{8}{S_{ABC}}\](do tam giác BMNBMN và tam giác BACBAC đồng dạng theo tỉ số\[DH \bot \left( {ABC} \right)\])
Do đó\[{V_{S.BMN}} = \frac{1}{8}{V_{S.ABCD}} = \frac{1}{8}V\]
- Xét khối chóp S.IMN và S.AMN:
\[\frac{{{V_{S.IMN}}}}{{{V_{S.AMN}}}} = \frac{{SI}}{{SA}} = x \Rightarrow {V_{S.IMN}} = x.{V_{S.AMN}}\]
Ta có\[{S_{AMN}} = {S_{BMN}} = \frac{1}{8}{S_{ABCD}} \Rightarrow {V_{S.AMN}} = \frac{1}{8}V \Rightarrow {V_{S.IMN}} = \frac{x}{8}V\]
- Xét khối chóp S.INP và S.ANC:
\[\frac{{{V_{S.INP}}}}{{{V_{S.ANC}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}} = {x^2} \Rightarrow {V_{S.IMN}} = {x^2}.{V_{S.ANC}}\]
Ta có\[{S_{ANC}} = \frac{1}{2}{S_{ABC}} = \frac{1}{4}{S_{ABCD}} \Rightarrow {V_{S.ANC}} = \frac{1}{4}V \Rightarrow {V_{S.IMN}} = \frac{{{x^2}}}{4}V\]
- Xét khối chóp S.IPQ và S.ACD:\[\frac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}}\]
Ta có AMEC là hình bình hành nên\[EC = AM = \frac{1}{2}CD \Rightarrow \frac{{EC}}{{ED}} = \frac{1}{3}\]
Áp dụng định lí Menelaus trong tam giác SCD với cát tuyến EPQ ta có:
\[\frac{{PS}}{{PC}}.\frac{{EC}}{{ED}}.\frac{{QD}}{{QS}} = 1 \Rightarrow \frac{x}{{1 - x}}.\frac{1}{3}.\frac{{QD}}{{QS}} = 1\]
\[\begin{array}{*{20}{l}}{ \Rightarrow \frac{{QD}}{{QS}} = \frac{{3\left( {1 - x} \right)}}{x} \Rightarrow \frac{{SQ}}{{QD}} = \frac{x}{{3\left( {1 - x} \right)}}}\\{ \Rightarrow \frac{{SQ}}{{SQ + QD}} = \frac{x}{{x + 3\left( {1 - x} \right)}}}\\{ \Rightarrow \frac{{SQ}}{{SD}} = \frac{x}{{3 - 2x}}}\end{array}\]
Suy ra\[\frac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}} = {x^2}.\frac{x}{{3 - 2x}} = \frac{{{x^3}}}{{3 - 2x}}\]
\[ \Rightarrow {V_{S.IPQ}} = \frac{{{x^3}}}{{3 - 2x}}{V_{S.ACD}}\]
Mà\[{S_{ACD}} = \frac{1}{2}{S_{ABCD}} \Rightarrow {V_{S.ACD}} = \frac{1}{2}V \Rightarrow {V_{S.IPQ}} = \frac{{{x^3}}}{{2\left( {3 - 2x} \right)}}V\]
Khi đó ta có:
\[{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\]
\[ \Rightarrow {V_1} = \frac{1}{8}V + \frac{x}{8}V + \frac{{{x^2}}}{4}V + \frac{{{x^3}}}{{2(3 - 2x)}}V\]
\[\begin{array}{l} \Rightarrow {V_1} = \left( {\frac{1}{8} + \frac{x}{8} + \frac{{{x^2}}}{4} + \frac{{{x^3}}}{{2(3 - 2x)}}} \right)V = \frac{7}{{32}}V\\ \Rightarrow \frac{1}{8} + \frac{x}{8} + \frac{{{x^2}}}{4} + \frac{{{x^3}}}{{2(3 - 2x)}} = \frac{7}{{32}}\\ \Leftrightarrow \frac{{1 + x + 2x2}}{4} + \frac{{{x^3}}}{{3 - 2x}} = \frac{7}{{16}}\\ \Leftrightarrow (1 + x + 2{x^2}).(12 - 8x) + 16{x^3} = 7(3 - 2x)\\ \Leftrightarrow 12 + 12x + 24{x^2} - 8x - 8{x^2} - 16{x^3} + 16{x^3} = 21 - 14x\\ \Leftrightarrow 16{x^2} + 18x - 9 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{3}{8}\left( {tm} \right)}\\{x = - \frac{3}{2}\left( {ktm} \right)}\end{array}} \right.\end{array}\]
\[ \Rightarrow \frac{{SI}}{{SA}} = \frac{3}{8} \Rightarrow \frac{{IS}}{{IA}} = \frac{3}{5} \Rightarrow \frac{{IA}}{{IS}} = \frac{5}{3}\]
Đáp án cần chọn là: A
Câu 2
A.\[\frac{{{a^3}\sqrt 2 }}{6}\]
B. \[\frac{{{a^3}\sqrt 3 }}{6}\]
C. \[\frac{{{a^3}\sqrt 3 }}{{12}}\]
D. \[\frac{{{a^3}\sqrt 2 }}{{12}}\]
Lời giải
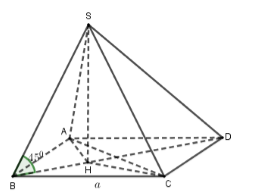
Gọi H là hình chiếu của S lên (ABCD).
Khi đó, \[\widehat {SAH} = \widehat {SCH}\] vì hai góc này lần lượt là góc tạo bởi SA,SC với mặt phẳng đáy.
\[\widehat {SBH} = {45^0},\tan \widehat {SDH} = \frac{1}{3}\]
Tam giác\[{\rm{\Delta }}SAH = {\rm{\Delta }}SCH \Rightarrow HA = HC \Rightarrow H\] nằm trên trung trực của AC.
Mà BD là đường trung trực của AC nên\[H \in BD\]
Lại có\[\widehat {SBH} = {45^0} \Rightarrow HB = HS,\tan \widehat {SDH} = \frac{1}{3} = \frac{{SH}}{{HD}}\]
\[ \Rightarrow \frac{{HB}}{{HD}} = \frac{1}{3} \Rightarrow \frac{{HB}}{{BD}} = \frac{1}{4}\]
Mà\[BD = a\sqrt 2 \Rightarrow HB = \frac{{a\sqrt 2 }}{4} \Rightarrow SH = \frac{{a\sqrt 2 }}{4}\]
Vậy\[{V_{S.ABCD}} = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{4}.{a^2} = \frac{{{a^3}\sqrt 2 }}{{12}}\]
Đáp án cần chọn là: D
Câu 3
A.\[2\sqrt 6 {a^3}\]
B. \[8{a^3}\]
C. \[\frac{{2\sqrt 6 }}{3}{a^3}\]
D. \[\frac{{7{a^3}}}{{12}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[\frac{{{a^3}}}{6}\]
B. \[\frac{{{a^3}}}{3}\]
C. \[\frac{{{a^3}}}{4}\]
D. \[\frac{{{a^3}}}{8}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[\frac{{5{a^3}\sqrt 2 }}{{12}}\]
B. \[\frac{{5{a^3}\sqrt 2 }}{6}\]
C. \[\frac{{5{a^3}\sqrt 2 }}{8}\]
D. \[\frac{{5{a^3}\sqrt 2 }}{{24}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[\frac{{{a^3}\sqrt 3 }}{{12}}\]
B. \[\frac{{{a^3}\sqrt 3 }}{{24}}\]
C. \[\frac{{{a^3}\sqrt 3 }}{6}\]
D. \[\frac{{{a^3}\sqrt 3 }}{8}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.