20 câu Trắc nghiệm Toán 11 Cánh diều Bài 3. Hàm số liên tục (Đúng-sai, trả lời ngắn) có đáp án
33 người thi tuần này 4.6 278 lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
B
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm của khoảng đó.
Câu 2
Lời giải
B
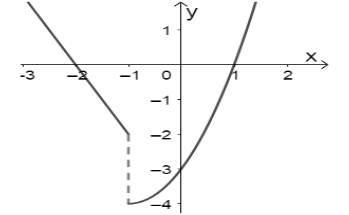
Dựa vào đồ thị hàm số y = f(x), ta thấy hàm số f(x) liên tục tại x = 1.
Câu 3
Lời giải
A
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Câu 4
Lời giải
D
Hàm số \(f\left( x \right) = \frac{1}{x}\) không xác định tại x = 0. Do đó f(x) liên tục trên (−∞; 0) và (0; +∞).
Câu 5
Lời giải
A
Hàm phân thức \(y = \frac{1}{{{x^2} - 3x + 2}}\) liên tục trên mỗi khoảng xác định (−∞; 1); (1; 2) và (2; +∞).
Câu 6
A. \(y = \frac{{{x^2} + 2x - 1}}{{x + 1}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(f\left( x \right) = \frac{{x + 1}}{{{x^2}}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(f\left( x \right) = \frac{{2{x^2} - 5x + 2}}{{{x^2} - 4}}\).
a) Hàm số f(x) liên tục trên khoảng (3; +∞).
b) Hàm số f(x) liên tục tại x = −2.
c) Hàm số f(x) gián đoạn tại x = 2.
d) Nếu \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \frac{a}{b}\) với a, b Î ℤ; \(\frac{a}{b}\) tối giản thì a2 + b2 = 25.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(f\left( x \right) = \frac{{2{x^2} - 5x + 2}}{{{x^2} - 4}}\).
a) Hàm số f(x) liên tục trên khoảng (3; +∞).
b) Hàm số f(x) liên tục tại x = −2.
c) Hàm số f(x) gián đoạn tại x = 2.
d) Nếu \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \frac{a}{b}\) với a, b Î ℤ; \(\frac{a}{b}\) tối giản thì a2 + b2 = 25.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}} & {\rm{khi}}\,x \ne 1\\x + 1 & {\rm{khi}}\,x = 1\end{array} \right.\) và \(g(x) = 4{x^2} - x + 1\). Khi đó:
a) Ta có \(f(1) = 2\).
b) Hàm số \(f\left( x \right)\) liên tục tại điểm \({x_0} = 1\).
c) Hàm số \(g\left( x \right)\)liên tục tại điểm \({x_0} = 1\).
d) Hàm số \(y = f\left( x \right) - g\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}} & {\rm{khi}}\,x \ne 1\\x + 1 & {\rm{khi}}\,x = 1\end{array} \right.\) và \(g(x) = 4{x^2} - x + 1\). Khi đó:
a) Ta có \(f(1) = 2\).
b) Hàm số \(f\left( x \right)\) liên tục tại điểm \({x_0} = 1\).
c) Hàm số \(g\left( x \right)\)liên tục tại điểm \({x_0} = 1\).
d) Hàm số \(y = f\left( x \right) - g\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Cho hàm số \(y = f\left( x \right) = \frac{{3x + 1}}{{x - 1}}\). Khi đó:
a) \[\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \].
b) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 4\).
c) Hàm số y = f(x) liên tục tại điểm x0 = 1.
d) Hàm số y = f(x) liên tục trên từng khoảng (−∞; 1) và (1; +∞).
Cho hàm số \(y = f\left( x \right) = \frac{{3x + 1}}{{x - 1}}\). Khi đó:
a) \[\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \].
b) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 4\).
c) Hàm số y = f(x) liên tục tại điểm x0 = 1.
d) Hàm số y = f(x) liên tục trên từng khoảng (−∞; 1) và (1; +∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.