Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3;−4), B(1;5) và C(3;1). Tính diện tích tam giác ABC.
A.10.
B.5.
C.\[\sqrt {26} .\]
D. \[2\sqrt 5 .\]
Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Khoảng cách và góc !!
Quảng cáo
Trả lời:
Cách 1:
+) Viết phương trình BCBC:
Ta có:\[\overrightarrow {BC} = \left( {2; - 4} \right)\] nên\[\overrightarrow {{u_{BC}}} = \frac{1}{2}\overrightarrow {BC} = \left( {1; - 2} \right)\] là VTCP của BC, do đó\[\overrightarrow {{n_{BC}}} = \left( {2;1} \right)\]
Đường thẳng BC đi qua B(1;5) và nhận\[\overrightarrow {{n_{BC}}} = \left( {2;1} \right)\] làm VTPT nên:
\[BC:2\left( {x - 1} \right) + 1\left( {y - 5} \right) = 0\] hay\[BC:2x + y - 7 = 0\]
Suy ra
\(\left\{ {\begin{array}{*{20}{c}}{A(3; - 4)}\\{B(1;5),C(3;1)}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{A(3; - 4)}\\{BC = 2\sqrt 5 }\\{BC:2x + y - 7 = 0}\end{array}} \right.\)
\( \to \left\{ {\begin{array}{*{20}{c}}{BC = 2\sqrt 5 }\\{hA = d(A;BC) = \sqrt 5 }\end{array}} \right.\)
\[ \to {S_{ABC}} = \frac{1}{2}.2\sqrt 5 .\sqrt 5 = 5.\]
Đáp án cần chọn là: B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[x - 4y + 19 = 0\;\] hoặc y = 5
B.\[x - 4y + 19 = 0\]
C.\[x - 3y + 19 = 0\]
D.\[2x - 3y - 19 = 0\]
Lời giải
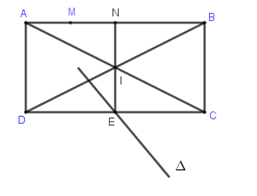
\[I\left( {6;2} \right);M\left( {1;5} \right)\]
\[{\rm{\Delta }}:x + y - 5 = 0,E \in {\rm{\Delta }} \Rightarrow E\left( {m;5 - m} \right);\]
Gọi N là trung điểm của AB
I trung điểm NE \( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{x_N} = 2{x_I} - {x_E} = 12 - m}\\{{y_N} = 2{y_I} - {y_E} = 4 - 5 + m = m - 1}\end{array}} \right.\)
\[ \Rightarrow N\left( {12 - m;m - 1} \right)\]
\[\overrightarrow {MN} = \left( {11 - m;m - 6} \right);\]
\[\overrightarrow {IE} = \left( {m - 6;5 - m - 2} \right) = \left( {m - 6;3 - m} \right)\]
\[\overrightarrow {MN} .\overrightarrow {IE} = 0 \Leftrightarrow \left( {11 - m} \right)\left( {m - 6} \right) + \left( {m - 6} \right)\left( {3 - m} \right) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m - 6 = 0}\\{14 - 2m = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 6}\\{m = 7}\end{array}} \right.\)
\[m = 6 \Rightarrow \overrightarrow {MN} = \left( {5;0} \right)\]nên phương trình AB là y = 5
\[m = 7 \Rightarrow \overrightarrow {MN} = \left( {4;1} \right)\] nên phương trình AB là \[x - 4y + 19 = 0\]Đáp án cần chọn là: A
Câu 2
A.3x−y−6=0
B.x−y−16=0
C.−y−6=0
D.−x−7y−6=0
Lời giải
+ Cạnh AB đi qua hai điểm A,B nên phương trình cạnh AB:\[x - 2y - 2 = 0\]+ Cạnh AC đi qua hai điểm A,C nên phương trình cạnh \[AC:2x + y - 4 = 0\]+ Phương trình hai đường phân giác của góc A:
\(\frac{{x - 2y - 2}}{{\sqrt 5 }} = \pm \frac{{2x + y - 4}}{{\sqrt 5 }} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 3y - 2 = 0(d)}\\{3x - y - 6 = 0(d\prime )}\end{array}} \right.\)
+ Xét đường phân giác \[\left( d \right):x + 3y - 2 = 0\]
Thế tọa độ điểm B vào vế trái của\[d:{t_1} = 4 + 3.1 - 2 = 5 >0\]
Thế tạo độ điểm C vào vế trái của d: \[{t_2} = 1 + 3.2 - 2 = 5 >0\]
Vì\[{t_1}.{t_2} >0\] nên B và C nằm cùng phía đối với d⇒d là đường phân giác ngoài
Vậy đường phân giác trong của góc A là: \[d':3x - y - 6 = 0\]
Đáp án cần chọn là: A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[x - 5y + 9 = 0\]
B. \[x - 5y + 9 = 0\]hoặc \[5x + y - 7 = 0\]
C.\[5x + y + 7 = 0\]
D.\[x - 5y + 19 = 0\;\] hoặc \[ - 5x + y + 7 = 0\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[\frac{{12}}{{\sqrt 5 }}\] (đvdt)
B.\[\frac{{16}}{5}\] (đvdt)
C.\[\frac{9}{5}\] (đvdt)
D.\[\frac{{12}}{5}\] (đvdt)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.x+2y−7=0
B.5x+2y+7=0
C.x+2y+7=0
D.2x+5y+7=0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.m = 2.
B.
C. \[m = - \frac{1}{2}\]
D. Không tồn tại m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.