Cho tứ diện ABCD. Gọi E,F,G là các điểm lần lượt thuộc các cạnh AB,AC,BD sao cho EF cắt BC tại I, EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?
A.CD,EF,EG.
B.CD,IG,HF.
C.AB,IG,HF.
D.AC,IG,BD.
Quảng cáo
Trả lời:
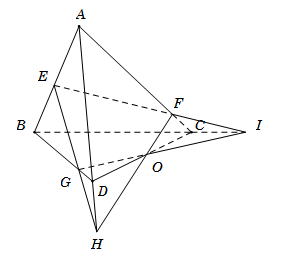
Trong\[mp(EHI)\], gọi\[O = HF \cap IG\] Ta có
● \[O \in HF\] mà \[HF \subset \left( {ACD} \right)\] suy ra \[O \in \left( {ACD} \right)\].
● \[O \in IG\] mà \[IG \subset \left( {BCD} \right)\] suy ra \[O \in \left( {BCD} \right)\]
Do đó \[O \in \left( {ACD} \right) \cap \left( {BCD} \right)\] (1)
Mà \[\left( {ACD} \right) \cap \left( {BCD} \right) = CD\](2)
Từ (1) và (2), suy ra \[O \in CD\]
Vậy ba đường thẳng CD,IG,HF đồng quy.
Đáp án cần chọn là: B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[AM = \left( {ACD} \right) \cap \left( {ABG} \right).\]
B.A,J,M thẳng hàng
C.J là trung điểm của AM.
D.\[DJ = \left( {ACD} \right) \cap \left( {BDJ} \right).\]
Lời giải

Ta có A là điểm chung thứ nhất giữa hai mặt phẳng (ACD) và (GAB).
Do\[BG \cap CD = M \Rightarrow \left\{ {\begin{array}{*{20}{c}}{M \in BG \subset (ABG) \Rightarrow M \in (ABG)}\\{M \in CD \subset (ACD) \Rightarrow M \in (ACD)}\end{array}} \right.\]
⇒M là điểm chung thứ hai giữa hai mặt phẳng (ACD) và (GAB).
\[ \Rightarrow \left( {ABG} \right) \cap \left( {ACD} \right) = AM\mathop \to \limits^{} \] A đúng.
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BI \subset (ABG)}\\{AM \subset (ABM)}\\{(ABG) \equiv (ABM)}\end{array}} \right. \Rightarrow AM,BI\) đồng phẳng.
\[ \Rightarrow J = BI \cap AM \Rightarrow A,J,M\] thẳng hàng→ B đúng.
Ta có \(\left\{ {\begin{array}{*{20}{c}}{DJ \subset (ACD)}\\{DJ \subset (BDJ)}\end{array}} \right. \Rightarrow DJ = (ACD) \cap (BDJ) \to \) D đúng.
Điểm I di động trên AG nên J có thể không phải là trung điểm của AM
→ C sai
Đáp án cần chọn là: C
Câu 2
A.AB=BC
B.BC=AD
C.AC = BD
D.AB=CD
Lời giải
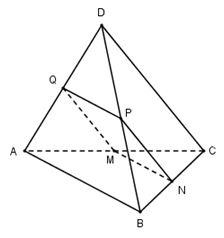
Vì MN và PQ lần lượt là đường trung bình của tam giác ABC và ABD nên:\(\left\{ {\begin{array}{*{20}{c}}{MN//PQ//AB}\\{MN = PQ = \frac{1}{2}AB}\end{array}} \right.\)=> MNPQ là hình bình hành.
Để MNPQ trở thành hình thoi ta cần thêm yếu tố \[MN = PN.\]
Ta có: PN là đường trung bình của tam giác BCD nên\[PN = \frac{1}{2}CD\]
\[MN = PN \Leftrightarrow \frac{1}{2}AB = \frac{1}{2}CD \Leftrightarrow AB = CD.\]
Vậy để MNPQ là hình thoi cần thêm điều kiện AB=CD.
Đáp án cần chọn là: D
Câu 3
A.\[\frac{{SQ}}{{SD}} = \frac{1}{4}.\]
B. \[\frac{{SQ}}{{SD}} = \frac{1}{3}.\]
C. \[\frac{{SQ}}{{SD}} = \frac{1}{5}.\]
D. \[\frac{{SQ}}{{SD}} = \frac{6}{{25}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.Ba đường thẳng AB,CD,MN đôi một song song
B.Ba đường thẳng AB,CD,MN đôi một cắt nhau
C.Ba đường thẳng AB,CD,MN đồng quy.
D.Ba đường thẳng AB,CD,MN cùng thuộc một mặt phẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.Hình thang
B.Hình bình hành
C.Hình chữ nhật
D.Tứ diện vì MN và BD chéo nhau
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.Chéo nhau
B.có hai điểm chung
C.song song
D.có một điểm chung
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.