Cho lăng trụ tam giác ABC.A′B′C′, gọi M,N lần lượt là hai điểm bất kỳ phân biệt nằm trên các cạnh AB′,A′B. Hình chiếu của chúng qua phép chiếu song song theo phương CC′ trên mặt phẳng (A′B′C′) lần lượt là M′,N′. Chọn kết luận không đúng:
A.M′N′//MN
B.M′N′⊂A′B′
C.MM′//AA′
D.M′N′//AB
Quảng cáo
Trả lời:
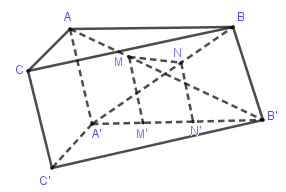
Qua M kẻ đường thẳng song song với AA′ cắt A′B′ tại MM′⇒MM′//AA′//CC′ nên M′ là hình chiếu của M qua phép chiếu bài cho.
Tương tự \[N' \in A'B'\] mà \[NN'//BB'\] cũng là ảnh của N qua phép chiếu bài cho.
Khi đó \[M'N' \subset A'B',MM'//AA',M'N'//AB\] nên các đáp án B, C, D đều đúng.
Đáp án A sai vì MN và M′N′ không song song.
Đáp án cần chọn là: A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\frac{3}{4}\]
b. \[\frac{1}{3}\]
c. \[\frac{1}{2}\]
d. \[\frac{2}{3}\]
Lời giải
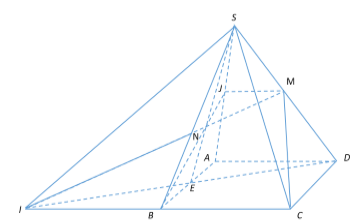
Gọi J;E lần lượt là trung điểm SA;AB.
Trong mặt phẳng (BCMJ) gọi \[I = MN \cap BC\]
Ta có: IM là đường trung tuyến của tam giác SID.
Trong tam giác ICD ta có BE song song và bằng\[\frac{1}{2}CD\] nên suy ra BE là đường trung bình của tam giác ICD⇒EI là trung điểm ID⇒SE là đường trung tuyến của tam giác SID.
Ta có: \[N = IM \cap SE \Rightarrow N\] là trọng tâm tam giác\[SID \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3}\]
Đáp án cần chọn là: D
Câu 2
A.Chéo nhau
B.đồng qui
C.Song song
D.thẳng hàng
Lời giải
Qua phép chiếu song song, tính chất chéo nhau không được bảo toàn.
Đáp án cần chọn là: A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.song song
B.trùng nhau
C.song song hoặc trùng nhau
D.cắt nhau
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.một đường thẳng
B.một đoạn thẳng
C.một mặt phẳng
D.một điểm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.