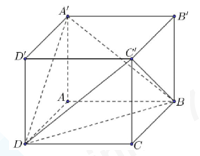
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \) cạnh bên AA′=a (minh họa như hình vẽ). Góc giữa hai mặt phẳng (A′BD) và (C′BD) bằng bao nhiêu độ?
Quảng cáo
Trả lời:
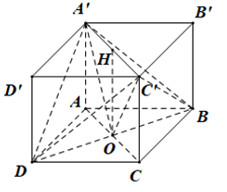
Bước 1: Xác định góc
Vì ABCD là hình vuông nên AC vuông góc BD tại O.
Suy ra \[BD \bot \left( {A'OC'} \right)\]. Góc giữa hai mặt phẳng\[\left( {A'BD} \right),\,\,\left( {C'BD} \right)\] là\[\angle A'OC'\]
Bước 2: Sử dụng tính chất tam giác vuông cân để tính góc.
Gọi H là tâm hình vuông A′B′C′D′ thì H là trung điểm A′C′ và\[\begin{array}{*{20}{l}}{OH = A'A = a}\\{A'H = HC' = \frac{{A'C'}}{2} = \frac{{A'B'\sqrt 2 }}{2} = \frac{{a\sqrt 2 .\sqrt 2 }}{2} = a}\end{array}\]
Suy ra các tam giác\[OHA';\,\,OHC'\] vuông cân và\[\angle A'OC' = {90^ \circ }\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\varphi = {90^0}.\]
B. \[\varphi = {60^0}.\]
C. \[\varphi = {45^0}.\]
D. \[\varphi = {30^0}.\]
Lời giải
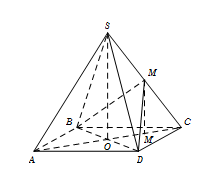
Gọi M’ là trung điểm\[OC \Rightarrow MM'\parallel SO \Rightarrow MM' \bot \left( {ABCD} \right).\]
Theo công thức diện tích hình chiếu, ta có\[{S_{{\rm{\Delta }}{\kern 1pt} M'BD}} = \cos \varphi .{S_{{\rm{\Delta }}{\kern 1pt} MBD}}\]
\[\begin{array}{*{20}{l}}{ \Rightarrow \cos \varphi = \frac{{{S_{{\rm{\Delta }}{\kern 1pt} M'BD}}}}{{{S_{{\rm{\Delta }}{\kern 1pt} MBD}}}} = \frac{{BD.M'O}}{{BD.MO}} = \frac{{M'O}}{{MO}} = \frac{{\frac{1}{2}OC}}{{\frac{1}{2}SA}}}\\{ = \frac{{\sqrt {B{C^2} - O{B^2}} }}{{SA}} = \frac{{\sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} }}{a} = \frac{{\sqrt 2 }}{2} \Rightarrow \varphi = {{45}^0}.}\end{array}\]
Đáp án cần chọn là: C
Lời giải
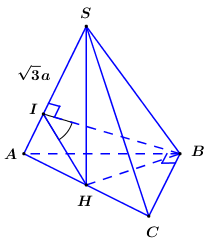
Bước 1: Gọi H là trung điểm của AC, chứng minh\[SH \bot \left( {SAC} \right),\,\,BH \bot \left( {SAC} \right)\]
Gọi H là trung điểm của AC ta có\[SH \bot AC\] (do tam giác SAC cân tại S).
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(SAC) \bot (ABC) = AC}\\{AH \subset (SAC),AH \bot AC}\end{array}} \right. \Rightarrow AH \bot \left( {ABC} \right)\). Tương tự \[BH \bot \left( {SAC} \right)\]
Bước 2: Trong (SAB) kẻ\[BI \bot SA\] chứng minh \[\angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {BH;HI} \right)\]
Trong (SAB) kẻ \[BI \bot SA\] ta có
\(\left\{ {\begin{array}{*{20}{c}}{SA \bot BI}\\{SA \bot BH(do\,BH \bot (SAC))}\end{array}} \right. \Rightarrow SA \bot (BHI) \Rightarrow SA \bot HI\)
\(\left\{ {\begin{array}{*{20}{c}}{(SAB) \cap (SAC) = SA}\\{BI \subset (SAB),BI \bot SA}\\{HI \subset (SAC),HI \bot SA}\end{array}} \right. \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {BI;HI} \right)\)
Bước 3: Sử dụng tính chất tam giác vuông cân, định lí Pytago, hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Vì\[BH \bot \left( {SAC} \right)\,\,\left( {cmt} \right) \Rightarrow BH \bot HI \Rightarrow {\rm{\Delta }}BHI\] vuông tại I.
Do đó\[\angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {BH;HI} \right) = \angle BHI\]
Tam giác ABC vuông cân tại B có\[AB = BC = 2a\] nên\[BH = \frac{{AB}}{{\sqrt 2 }} = a\sqrt 2 ,AC = AB\sqrt 2 = 2\sqrt 2 a\]
Ta có: \[SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {3{a^2} - 2{a^2}} = a\]
\[ \Rightarrow HI = \frac{{SH.AH}}{{SA}} = \frac{{a.\sqrt 2 a}}{{\sqrt 3 a}} = \frac{{\sqrt 6 a}}{3}\]Xét tam giác vuông BHI có\[\tan \angle BIH = \frac{{BH}}{{IH}} = \frac{{a\sqrt 2 }}{{\frac{{\sqrt 6 a}}{3}}} = \sqrt 3 \Rightarrow \angle BIH = {60^0}\]
Vậy góc giữa mặt phẳng (SAB) và (SAC) là 600
Câu 3
A.\[\cos \alpha = \frac{1}{3}.\]
B. \[\cos \alpha = \frac{{\sqrt 2 }}{3}.\]
C. \[\cos \alpha = \frac{{\sqrt 3 }}{3}.\]
D. \[\cos \alpha = \frac{2}{3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[\widehat {CSF}.\]
B. \[\widehat {BSF}.\]
C. \[\widehat {BSE}.\]
D. \[\widehat {CSE}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[x = \frac{{3a}}{2}.\]
B. \[x = \frac{a}{2}.\]
C. \[x = a.\]
D. \[x = 2a.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[\cot \varphi = \frac{{\sqrt 2 }}{4}.\]
B. \[\cot \varphi = \sqrt 7 .\]
C. \[\cot \varphi = \frac{{\sqrt 7 }}{7}.\]
D. \[\cot \varphi = \frac{{\sqrt {14} }}{4}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.