Cho hàm số y=f(x). Hàm số y=f′(x) có đồ thị như hình bên. Biết \[f\left( { - 1} \right) = 1,f( - \frac{1}{e}) = 2.\]. Tìm tất cả các giá trị của m để bất phương trình \[f(x) < ln( - x) + m\;\] nghiệm đúng với mọi \[x \in ( - 1; - \frac{1}{e}).\]
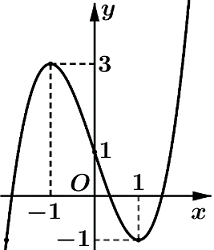
A.\[m \ge 2.\]
B. \[m \ge 3.\]
C. \[m > 2.\]
D. \[m > 3.\]
Quảng cáo
Trả lời:
ĐKXĐ: \[ - x > 0 \Leftrightarrow x < 0\]
Ta có: \[f\left( x \right) < \ln \left( { - x} \right) + m \Leftrightarrow m > f\left( x \right) - \ln \left( { - x} \right)\left( * \right)\]</>
Xét hàm số \[g\left( x \right) = f\left( x \right) - \ln \left( { - x} \right)\] trên khoảng \[\left( { - 1; - \frac{1}{e}} \right)\] có:
\[\,g'\left( x \right) = f'\left( x \right) - \frac{{ - 1}}{{ - x}} = f'\left( x \right) - \frac{1}{x}\]
Ta biểu diễn đồ thị hàm số\[y = \frac{1}{x}\] (nét màu đỏ) trên hình vẽ như sau:
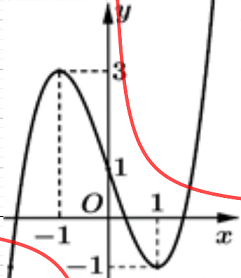
Quan sát đồ thị hàm số ta thấy
\[\,g'\left( x \right) = f'\left( x \right) - \frac{1}{x} > 0,\,\,\forall x \in \left( { - 1; - \frac{1}{e}} \right) \Rightarrow \] Hàm số\[y = g\left( x \right)\] đồng biến trên\[\left( { - 1; - \frac{1}{e}} \right)\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{g( - 1) = f( - 1) - ln(1) = 1}\\{g( - \frac{1}{e}) = f( - \frac{1}{e}) - ln\frac{1}{e} = 2 + 1 = 3}\end{array}} \right.\)
Để (*) nghiệm đúng với mọi\[x \in \left( { - 1; - \frac{1}{e}} \right)\] thì \[ \Leftrightarrow m \ge \mathop {max}\limits_{\left[ { - 1; - \frac{1}{e}} \right]} g\left( x \right) \Leftrightarrow m \ge 3.\]
Đáp án cần chọn là: B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Bước 1: Đặt\[f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\] và tìm điều kiện xác định.
Đặt\[f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\] (coi yy là tham số).
Điều kiện xác định của f(x) là:
\(\left\{ {\begin{array}{*{20}{c}}{x + {y^2} > 0}\\{{y^2} + y + 64 > 0}\\{x - y > 0}\end{array}} \right.\)
Do x,y nguyên nên\[x > y \ge - {y^2}\] Cũng vì x,y nguyên nên ta chỉ xét f(x) trên nửa khoảng \[\left[ {y + 1; + \infty } \right)\]
Bước 2: Xét hàm số trên\[\left[ {y + 1; + \infty } \right)\]
Ta có:
\[f'\left( x \right) = \frac{1}{{\left( {x + {y^2}} \right)\ln 2020}} - \frac{1}{{\left( {x - y} \right)\ln 2021}} - \frac{1}{{\left( {x - y} \right)\ln 4}} < 0,\;\forall x \ge y + 1\]
Bước 3: Lập bảng biến thiên
Ta có bảng biến thiên của hàm số f(x):
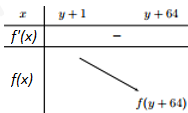
Bước 4: Tìm y nguyên \[f\left( {y + 64} \right) < 0\]
Yêu cầu bài toán trở thành:
\[f\left( {y + 64} \right) < 0\]
\[ \Leftrightarrow {\log _{2020}}\left( {{y^2} + y + 64} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) < {\log _4}64\]
\[ \Leftrightarrow {\log _{2021}}\left( {{y^2} + y + 64} \right)\left( {{{\log }_{2020}}2021 + 1} \right) < 3\]
\[ \Leftrightarrow {y^2} + y + 64 - {2021^{\frac{3}{{{{\log }_{2020}}2021 + 1}}}} < 0\]
\[ \Leftrightarrow - 301,76 < y < 300,76\]
Mà y nguyên nên\[y \in \left\{ { - 301; - 300; \ldots ;299;300} \right\}\]
Vậy có 602 giá trị nguyên của yy thỏa mãn yêu cầu.
Câu 2
A.403,32 (triệu đồng).
B.293,32 (triệu đồng).
C.412,23 (triệu đồng).
D.393,12 (triệu đồng).
Lời giải
Gọi số tiền đóng hàng năm là A=12 (triệu đồng), lãi suất là\[r = 6{\rm{\% }} = 0,06\]
Sau 1 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là\[{A_1} = A\left( {1 + r} \right)\] (nhưng người đó không rút mà lại đóng thêm A triệu đồng nữa, nên số tiền gốc để tính lãi năm sau là\[{A_1} + A\])
Sau 2 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\[{A_2} = \left( {{A_1} + A} \right)\left( {1 + r} \right) = \left[ {A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right) = A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\]
Sau 3 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\[\begin{array}{l}{A_3} = \left( {{A_2} + A} \right)\left( {1 + r} \right) = \left[ {A{{\left( {1 + r} \right)}^2} + A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right)\\ = A{\left( {1 + r} \right)^3} + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\end{array}\]
Sau 18 năm, người đó đi rút tiền thì sẽ nhận được số tiền là:
\[{A_{18}} = A{\left( {1 + r} \right)^{18}} + A{\left( {1 + r} \right)^{17}} + ... + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\]
Tính:\[{A_{18}} = A\left[ {{{\left( {1 + r} \right)}^{18}} + {{\left( {1 + r} \right)}^{17}} + ... + {{\left( {1 + r} \right)}^2} + \left( {1 + r} \right) + 1 - 1} \right]\]
\[ \Rightarrow {A_{18}} = A\left[ {\frac{{{{\left( {1 + r} \right)}^{19}} - 1}}{{\left( {1 + r} \right) - 1}} - 1} \right] = A\left[ {\frac{{{{\left( {1 + r} \right)}^{19}} - 1}}{r} - 1} \right] = 12\left[ {\frac{{{{\left( {1 + 0,06} \right)}^{19}} - 1}}{{0,06}} - 1} \right] \approx 393,12\]
Đáp án cần chọn là: D
Câu 3
Tập nghiệm của bất phương trình \[\log \left( {{x^2} + 25} \right) > \log \left( {10x} \right)\] là:
A.\[R \setminus \left\{ 5 \right\}\]
B. \[\left( {0;5} \right) \cup \left( {5; + \infty } \right)\]
C. R
D. \[\left( {0; + \infty } \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[m \in \left( {0; + \infty } \right)\]
B. \[m \in \left( { - \frac{3}{4};0} \right)\]
C. \[m \in \left( { - \frac{3}{4}; + \infty } \right)\]
D. \[m \in \left( { - \infty ;0} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[S = ( - 2;0) \cup (\frac{1}{3};\,\,3\,]\]
B. \[S = ( - 1;0) \cup (\frac{1}{3};\,\,2\,]\,.\]
C. \[S = \left[ { - 1\,,\,0} \right) \cup (\frac{1}{3};\,\,3\,]\]
D. \[S = ( - 1;0) \cup (1;\,\,3\,]\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.