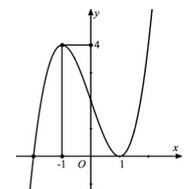
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số \[y = m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1\] có hai điểm cực trị nằm về hai phía của trục hoành.
A.3
B.2
C.1
D.4
Quảng cáo
Trả lời:
Để đồ thị hàm số\[y = m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1\] có hai điểm cực trị nằm về hai phía của trục hoành thì phương trình\[m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1 = 0\,\,\left( * \right)\] phải có 3 nghiệm phân biệt.
Ta có:
\[\begin{array}{l}m{x^3} - (2m - 1){x^2} + 2mx - m - 1 = 0\\ \Leftrightarrow (x - 1)[m{x^2} - (m - 1)x + m + 1] = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{m{x^2} - (m - 1)x + m + 1 = 0( * * )}\end{array}} \right.\end{array}\]
Để (*) có ba nghiệm phân biệt thì (**) phải có 2 nghiệm phân biệt khác 1.
\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{m.1 - (m - 1).1 + m + 1 \ne 0}\\{\Delta = {{(m - 1)}^2} - 4m(m + 1) > 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{m - m + 1 + m + 1 \ne 0}\\{{m^2} - 2m + 1 - 4{m^2} - 4m > 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{m \ne - 2}\\{ - 3{m^2} - 6m + 1 > 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{m \ne - 2}\\{\frac{{ - 3 - 2\sqrt 3 }}{3} < m < \frac{{ - 3 + 2\sqrt 3 }}{3}}\end{array}} \right.\end{array}\)
Mà\[m \in \mathbb{Z} \Rightarrow m = - 1\]
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số \[f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\] ta có
\[\begin{array}{l}f\prime (x) = 12{x^3} - 12{x^2} - 24x\\f\prime (x) = 0 \Leftrightarrow 12{x^3} - 12{x^2} - 24x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = - 1}\\{x = 2}\end{array}} \right.\end{array}\]
BBT:
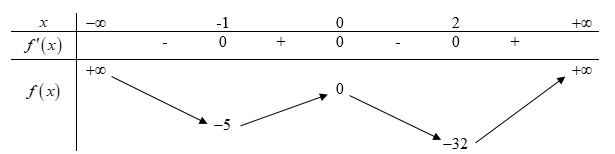
Ta có đồ thị \[y = f\left( x \right)\,\,\left( C \right)\] như sau:
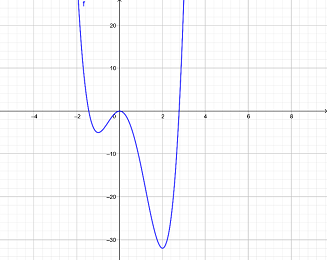
Để\[y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\] có 5 điểm cực trị thì:
TH1: (C) cắt đường thẳng y=−m tại 2 điểm phân biệt khác cực trị
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - m > 0}\\{ - 32 < - m < - 5}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m < 0}\\{5 < m < 32}\end{array}} \right.\)
Mà\[m \in {\mathbb{Z}^ + }\, \Rightarrow m \in \left\{ {6;7;...;31} \right\}\] 26 giá trị.
TH2: (C) cắt đường thẳng y=−m tại 3 điểm phân biệt, trong đó có 1 cực trị
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - m = 0}\\{ - m = - 5}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 0(L)}\\{m = 5(TM)}\end{array}} \right.\)
Vậy, có tất cả 27 giá trị của m thỏa mãn.
Đáp án cần chọn là: B
Lời giải
Bước 1:
Số điểm cực trị của hàm số\[y = f\left( {\left| x \right|} \right)\] là \[2m + 1\] trong đó m là số điềm cực trị dương của hàm số\[y = f\left( x \right)\]
Do đó để hàm số\[y = f\left( {\left| x \right|} \right)\] có đúng 3 điểm cực trị thì m=1⇒ hàm số\[y = f\left( x \right)\] phải có 1 điểm cực trị dương (*).
Bước 2:
Ta có:\[f'\left( x \right) = {x^2} + 2mx + {m^2} - 4\]
Xét\[f'\left( x \right) = 0\] có\[{\rm{\Delta '}} = {m^2} - {m^2} + 4 > 0\,\,\forall m\] nên\[f'\left( x \right) = 0\] có 2 nghiệm phân biệt
\(\left[ {\begin{array}{*{20}{c}}{{x_1} = - m + 2}\\{{x_2} = - m - 2}\end{array}} \right.\)
Bước 3:
\[\left( * \right) \Rightarrow - m - 2 \le 0 < - m + 2 \Leftrightarrow - 2 \le m < 2\]
Mà \[m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1} \right\}\]
Vậy có 4 giá trị của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: C
Câu 3
A.m=−4
B.m=−1
C.m=1
D.m=3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.m<0
B.m=0
C.m>0
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[y = mx + 3m - 1\]
B. \[y = - 2\left( {{m^2} + 1} \right)x + m\]
C. \[y = \left( {2{m^3} - 2} \right)x\]
D. \[y = - 2x + 2m\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.