3 bài tập Sự tương giao của đồ thị hàm số (có lời giải)
41 người thi tuần này 4.6 76 lượt thi 3 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Lời giải
Lập bảng:
Đường thẳng \[\left( d \right):\]
|
x |
0 |
4 |
|
\[y = \frac{{ - 1}}{2}x + 2.\] |
2 |
0 |
Parabol \[\left( P \right):\]
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
\[y = \frac{1}{4}{x^2}\] |
1 |
\[\frac{1}{4}\] |
0 |
\[\frac{1}{4}\] |
1 |
Vẽ đồ thị:
![Trong mặt phẳng tọa độ \[Oxy\], c (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/1-1769595332.png)
b) Tìm tọa độ giao điểm của \((P)\) và \((d)\) bằng phép tính.
Hoành độ giao điểm của \((P)\) và \((d)\) là nghiệm của phương trình
\[\frac{1}{4}{x^2} = - \frac{1}{2}x + 2\]
\[{x^2} + 2x - 8 = 0\]
\[\Delta ' = {1^2} - \left( { - 8} \right) = 9 > 0\]
Do \[\Delta ' > 0\] nên phương trình đã cho có hai nghiệm phân biệt là
\[x = - 4\] và \[x = 2\]
+ Với \[x = - 4 \Rightarrow y = 4\]
+ Với \[x = 2 \Rightarrow y = 1\].
Vậy tọa độ giao điểm của \((P)\) và \((d)\) là \(( - 4;4)\) và \(\left( {2;1} \right)\).
Lời giải
a) Vẽ parabol \((P)\) và đường thẳng \(d\) trên cùng một hệ trục tọa độ \(Oxy\)
Tập xác định: \(D = \mathbb{R}\)
\(a = 2 > 0\), hàm số đồng biến nếu \(x > 0\), hàm số nghịch biến nếu \(x < 0\)
Bảng giá trị
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = 2{x^2}\) |
\(8\) |
\(2\) |
\(0\) |
\(2\) |
\(8\) |
Đồ thị hàm số \(y = 2{x^2}\) là đường cong Parabol đi qua điểm \(O\), nhận \(Oy\) làm trục đối xứng, bề lõm hướng lên trên.
Tập xác định: \(D = \mathbb{R}\)
\(a = 1 > 0\) nên hàm số đồng biến trên \(\mathbb{R}\)
Đồ thị hàm số \(y = x + 1\) là đường thẳng đi qua điểm \((0;1)\) và \(( - 1;0)\)
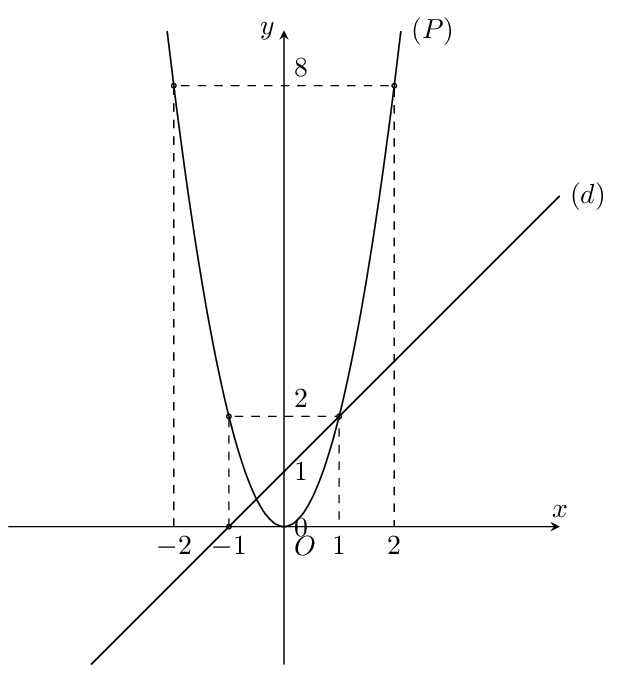
b) Tìm tọa độ giao điểm của \((P)\) và \((d)\) bằng phép tính.
Hoành độ giao điểm của \((P)\) và \((d)\) là nghiệm của phương trình
\(\begin{array}{l}2{x^2} = x + 1\\2{x^2} - x - 1 = 0\end{array}\).
Ta có \(a + b + c = 2 - 1 - 1 = 0\) nên phương trình có 2 nghiệm phân biệt \(x = 1\) và \(x = \frac{c}{a} = - \frac{1}{2}\)
+ Với \(x = 1 \Rightarrow y = 1 + 1 = 2\)
+ Với \(x = - \frac{1}{2} \Rightarrow y = - \frac{1}{2} + 1 = \frac{1}{2}\).
Vậy tọa độ giao điểm của \((P)\) và \((d)\) là \((1;2)\) và \(\left( { - \frac{1}{2};\frac{1}{2}} \right)\).
Lời giải
a) Vẽ đồ thị \(\left( P \right)\).
Đồ thị hàm số \(y = - {x^2}\) đi qua gốc tọa độ \(O\), có bề lõm hướng xuống và nhận \(Oy\) làm trục đối xứng.
Bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = - {x^2}\) |
\( - 4\) |
\( - 1\) |
0 |
\( - 1\) |
\( - 4\) |
\( \Rightarrow \) Parabol \(\left( P \right):y = - {x^2}\) đi qua các điểm \(\left( { - 2; - 4} \right)\), \(\left( { - 1; - 1} \right)\), \(\left( {0;0} \right)\), \(\left( {1; - 1} \right)\), \(\left( {2; - 4} \right)\).
Đồ thị Parabol \(\left( P \right):y = - {x^2}\) :
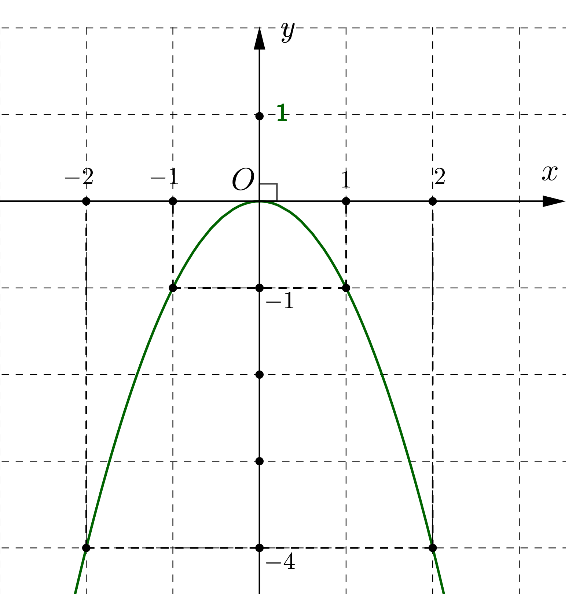
b) Hoành độ giao điểm của đồ thị \((P)\) và \((d)\)là nghiệm của phương trình:
\( - {x^2} = 5x + 6 \Leftrightarrow {x^2} + 5x + 6 = 0\)
Ta có: \({\rm{\Delta }} = {b^2} - 4ac = {5^2} - 4.6 = 1 > 0\) nên phương trình có 2 nghiệm phân biệt
\(\begin{array}{l}{x_1} = \frac{{ - 5 + 1}}{2} = - 2\\{x_2} = \frac{{ - 5 - 1}}{2} = - 3\end{array}\).
Với \({x_1} = - 2 \Rightarrow {y_1} = - {( - 2)^2} = - 4\).
Với \({x_2} = - 3 \Rightarrow {y_2} = - {( - 3)^2} = - 9\).
Vậy tọa độ các giao điểm của \(\left( P \right)\) và (d) là \(A\left( { - 2; - 4} \right),B\left( { - 3; - 9} \right)\).