Chuyên đề Toán 11 KNTT Bài 3. Phép đối xứng trục có đáp án
34 người thi tuần này 4.6 754 lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề chẵn
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề lẻ
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THCS & THPT Lương Thế Vinh (Hà Nội) có đáp án
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Nguyễn Gia Thiều (Hà Nội) có đáp án
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Hoài Đức A (Hà Nội) có đáp án
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phan Huy Chú (Đống Đa-Hà Nội) có đáp án
Danh sách câu hỏi:
Lời giải
Lời giải:
a) Đường thẳng giao bởi cầu và mặt nước trên dòng sông là trục đối xứng của hình ảnh đó (đường màu xanh trong hình vẽ).
b) Có thể đếm được 5 bóng điện dưới dòng sông. Mỗi hình đó là ảnh dưới sông của bóng điện tương ứng với từng số thứ tự trên cầu như ảnh.
Lời giải
Lời giải:
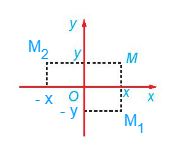
Từ hình vẽ ta thấy:
+) Phép đối xứng trục Ox biến mỗi điểm M(x; y) thành điểm M1(x; – y).
+) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm M2(– x; y).
Do đó, phép đối xứng trục Ox biến điểm A(1; 2) thành A'(1; – 2).
Vậy các khẳng định a), b) đúng và khẳng định c) sai.
Lời giải
Lời giải:
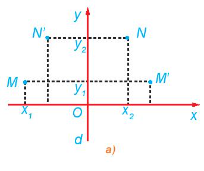
a) M' và N' lần lượt là ảnh của M và N qua phép đối xứng trục d (trục Oy).
Do đó M'(– x1; y1) và N'(– x2; y2).
b) Ta có: \(M{N^2} = {\left( {\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} } \right)^2}\)= (x2 – x1)2 + (y2 – y1)2
\(M'N{'^2} = {\left( {\sqrt {{{\left( { - {x_2} - \left( { - {x_1}} \right)} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} } \right)^2}\)= (– x2 + x1)2 + (y2 – y1)2.
c) Ta có: (x2 – x1)2 = (x1 – x2)2 = (– x2 + x1)2.
Do đó (x2 – x1)2 + (y2 – y1)2 = (– x2 + x1)2 + (y2 – y1)2 hay MN2 = M'N'2.
Suy ra MN = M'N'.
Lời giải
Lời giải:
Cách 1:
Lấy hai điểm A(0; – 1) và B(1; 2) thuộc d.
Gọi A', B' lần lượt là ảnh của A, B qua phép đối xứng trục Ox.
Khi đó A'(0; 1) và B'(1; – 2).
Vì d' là ảnh của đường thẳng d qua phép đối xứng trục Ox nên A' và B' thuộc d'.
Ta có: \(\overrightarrow {A'B'} = \left( {1;\, - 3} \right)\). Suy ra \(\overrightarrow {{n_{d'}}} = \left( {3;\,1} \right)\).
Vậy d' có phương trình là 3(x – 0) + (y – 1) = 0 hay 3x + y – 1 = 0.
Cách 2:
Gọi M'(x'; y') là ảnh của M(x; y) qua phép đối xứng trục Ox. Khi đó x' = x và y' = – y.
Ta có: M ∈ d ⇔ 3x – y – 1 = 0 ⇔ 3x' – (– y') – 1 = 0 ⇔ 3x' + y' – 1 = 0 ⇔ M' thuộc đường thẳng d' có phương trình là 3x + y – 1 = 0.
Lời giải
Lời giải:
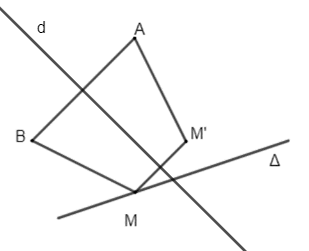
Gọi d là đường trung trực của đoạn thẳng AB. Vì AB cố định nên d cố định.
Do A, B, M, M' là 4 đỉnh của hình thang cân nhận AB là một cạnh đáy nên MM' là đáy còn lại của hình thang cân và đường trung trực d của đoạn thẳng AB cũng là đường trung trực của đoạn thẳng MM'. Do đó M' là ảnh của điểm M qua phép đối xứng trục d.
Mặt khác, M thuộc đường thẳng ∆ nên M' thuộc đường thẳng ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.
Vậy rằng M' thay đổi trên một đường thẳng cố định ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.
Lời giải
Lời giải:
Quan sát hình ảnh ta thấy hình thứ hai từ trái sang có trục đối xứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 5/11 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập