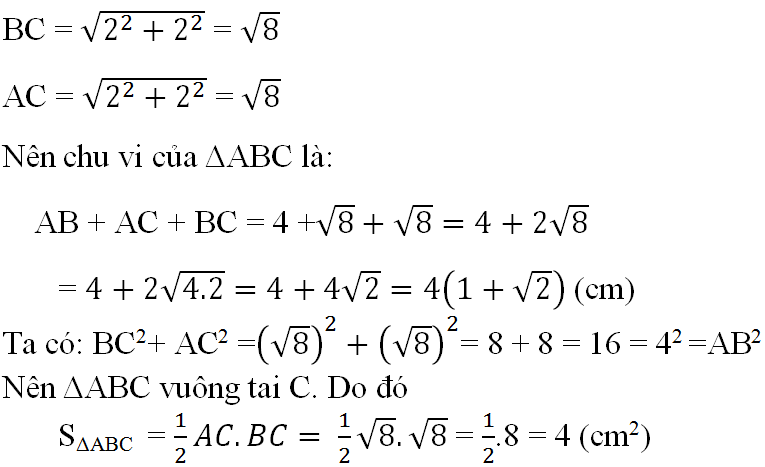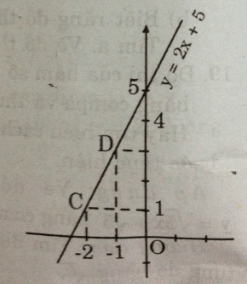Giải bài tập SGK Toán 9 tập 1 hay nhất Luyện tập trang 51-52
27 người thi tuần này 4.6 1.6 K lượt thi 3 câu hỏi
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
23 K lượt thi
3 câu hỏi
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
19.8 K lượt thi
20 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
6.5 K lượt thi
5 câu hỏi
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
1.7 K lượt thi
16 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
20.6 K lượt thi
4 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
3.5 K lượt thi
20 câu hỏi
123 bài tập Nón trụ cầu và hình khối có lời giải
1.2 K lượt thi
123 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
a) Vẽ đồ thị của các hàm số y = x + 1 và y = -x +3 trên cùng một mặt phẳng tọa độ.
b) Hai đường thẳng y = x + 1 và y = -x + 3 cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ các điểm A, B, C.
c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)
Lời giải
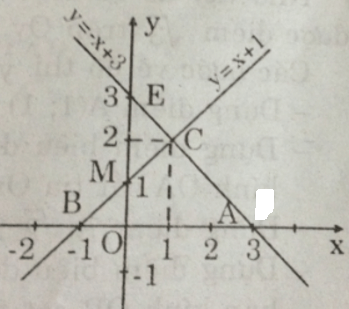
a) - Với hàm số y = x + 1:
Cho x = 0 => y = 1 ta được M(0; 1).
Cho y = 0 => x + 1 = 0 => x = -1 ta được B(-1; 0).
Nối MB ta được đồ thị hàm số y = x + 1.
- Với hàm số y = -x + 3:
Cho x = 0 => y = 3 ta được E(0; 3).
Cho y = 0 => -x + 3 = 0 => x = 3 ta được A(3; 0).
Nối EA ta được đồ thị hàm số y = -x + 3.
b) Từ hình vẽ ta có:
- Đường thẳng y = x + 1 cắt Ox tại B(-1; 0).
- Đường thẳng y = -x + 3 cắt Ox tại A(3; 0).
- Hoành độ giao điểm C của 2 đồ thị hàm số y = x + 1 và y = -x + 3 là nghiệm phương trình:
x + 1 = -x + 3
=> x = 1 => y = 2
=> Tọa độ C(1; 2)
c) Ta có: AB = 3 + 1 = 4
Câu 2
a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị B vừa tìm được.
b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1; 3). Tìm a. Vẽ đồ thị hàm số với giá trị a tìm được
Lời giải
a) Thay x = 4 và y = 11 vào y = 3x + b ta được:
11 = 3.4 + b = 12 + b
=> b = 11 – 12 = -1
Ta được hàm số y = 3x – 1
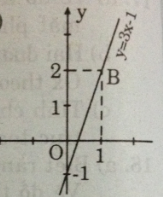
- Cho x = 0 => y = -1 được A(0; -1)
- Cho x = 1 => y = 2 được B(1; 2).
Nối A, B ta được đồ thị hàm số y = 3x – 1.
b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:
3 = a(-1) + 5
=> a = 5 – 3 = 2
Ta được hàm số y = 2x + 5.
- Cho x = -2 => y = 1 được C(-2; 1)
- Cho x = -1 => y = 3 được D(-1; 3)
Nối C, D ta được đồ thị hàm số y = 2x + 5.
Câu 3
Đồ thị của hàm số y = √3 x + √3 được vẽ bằng compa và thước thẳng (h.8).
Hãy thực hiện cách vẽ đó rồi nêu lại cách thực hiện.
Áp dụng: Vẽ đồ thị của hàm số y = √5 x + √5 bằng compa và thước thẳng.
Hướng dẫn: Tìm điểm trên trục tung có tung độ bằng √5.
Lời giải
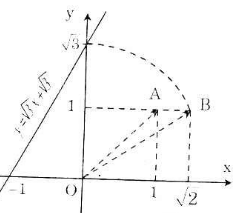
a) Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
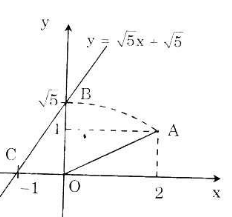
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.
4.6
329 Đánh giá
50%
40%
0%
0%
0%