Cho điểm M′ là hình chiếu của \[M \notin (\alpha )\;\] trên mặt phẳng (α) qua phép chiếu song song theo phương chiếu \[l \bot (\alpha ).\] Kết luận không đúng là:
A.MM′//l
B.MM′//(α)
C.\[MM\prime \bot (\alpha )\;\]
D.\[M\prime \in (\alpha )\;\]
Quảng cáo
Trả lời:
Vì M′ là hình chiếu của nên \[MM'//l\] nên A đúng.
Lại có \[l \bot \left( \alpha \right) \Rightarrow MM' \bot \left( \alpha \right)\] nên C đúng, B sai.
Hiển nhiên \[M' \in \left( \alpha \right)\] nên D đúng.
Đáp án cần chọn là: B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[\frac{3}{4}\]
b. \[\frac{1}{3}\]
c. \[\frac{1}{2}\]
d. \[\frac{2}{3}\]
Lời giải
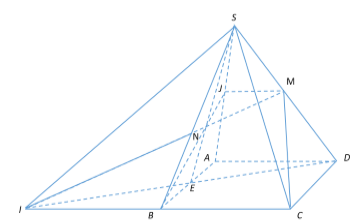
Gọi J;E lần lượt là trung điểm SA;AB.
Trong mặt phẳng (BCMJ) gọi \[I = MN \cap BC\]
Ta có: IM là đường trung tuyến của tam giác SID.
Trong tam giác ICD ta có BE song song và bằng\[\frac{1}{2}CD\] nên suy ra BE là đường trung bình của tam giác ICD⇒EI là trung điểm ID⇒SE là đường trung tuyến của tam giác SID.
Ta có: \[N = IM \cap SE \Rightarrow N\] là trọng tâm tam giác\[SID \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3}\]
Đáp án cần chọn là: D
Câu 2
A.Chéo nhau
B.đồng qui
C.Song song
D.thẳng hàng
Lời giải
Qua phép chiếu song song, tính chất chéo nhau không được bảo toàn.
Đáp án cần chọn là: A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.song song
B.trùng nhau
C.song song hoặc trùng nhau
D.cắt nhau
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.một đường thẳng
B.một đoạn thẳng
C.một mặt phẳng
D.một điểm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.