Cho hình lăng trụ tam giác đều ABC.A’B’C’, gọi G là trọng tâm tam giác ABC. (tham khảo hình vẽ). Khẳng định nào sau đây là sai?
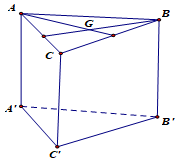
A.\[AG \bot B'C'\]
B. \[{\rm{AG}} \bot \left( {BCC'B'} \right)\]
C. \[{\rm{A}}{{\rm{A}}^\prime } \bot \left( {ABC} \right)\]
D. \[A'G \bot \left( {ABC} \right)\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Do ABC.A’B’C’ là hình lăng trụ tam giác đều nên \[BB' \bot \left( {ABC} \right)\]
\[ \Rightarrow BB' \bot AG\left( {AG \subset \left( {ABC} \right)} \right)\]Do ABC là tam giác đều nên G vừa là trọng tâm vừa là trực tâm. Do đó:
\(\begin{array}{l}\left. {\begin{array}{*{20}{c}}{AG \bot BC}\\{AG \bot BB\prime }\end{array}} \right\} \Rightarrow AG \bot (BCC\prime B\prime )\\ \Rightarrow AG \bot B\prime C\prime \end{array}\)
\[AA' \bot (ABC)\] vì \[ABC \cdot A'B'C'\] là hình lăng trụ đứng.
Đáp án cần chọn là: D
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
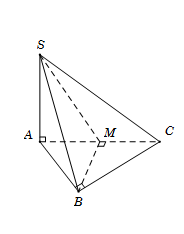
A.\[BM \bot AC.\]
B. \[\left( {SBM} \right) \bot \left( {SAC} \right).\]
C. \[\left( {SAB} \right) \bot \left( {SBC} \right).\]
D. \[\left( {SAB} \right) \bot \left( {SAC} \right).\]
Lời giải
Tam giác ABC cân tại B có M là trung điểm \[AC\,\, \Rightarrow \,\,BM \bot AC.\]
⇒ Đáp án A đúng.
Ta có
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{BM \bot AC}\\{BM \bot SA(doSA \bot (ABC))}\end{array}} \right. \Rightarrow BM \bot (SAC)\\ \Rightarrow (SBM) \bot (SAC)\end{array}\)
⇒ Đáp án B đúng.
Ta có
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{BC \bot BA}\\{BC \bot SA(doSA \bot (ABC))}\end{array}} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow (SBC) \bot (SAB)\end{array}\)
⇒ Đáp án C đúng.
Dùng phương pháp loại trừ thì D là đáp án sai.
Đáp án cần chọn là: D
Lời giải
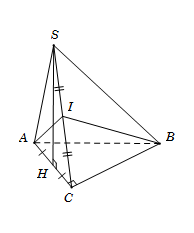
Tam giác SAC đều có I là trung điểm của SC nên \[AI \bot SC\].
⇒ Mệnh đề (I) đúng.
Gọi H là trung điểm AC suy ra \[SH \bot AC\]. Mà \[(SAC) \bot (ABC)\] theo giao tuyến AC nên \[SH \bot (ABC)\] do đó \[SH \bot BC\]. Hơn nữa theo giả thiết tam giác ABC vuông tại C nên \[BC \bot AC\].
Từ đó suy ra \[BC \bot (SAC) \Rightarrow BC \bot AI.\]. Do đó mệnh đề (III) đúng.
Từ mệnh đề (I) và (III) suy ra mệnh đề (IV) đúng.
Ta có : \(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{BC \bot AC}\\{BC \bot SH}\end{array}} \right. \Rightarrow BC \bot (SAC)\\BC \subset (SBC) \Rightarrow (SBC) \bot (SAC)\end{array}\)
Vậy mệnh đề (II) đúng.
Vậy mệnh đề (II) đúng.
Đáp án cần chọn là: D
Câu 3
A.\[SH \bot AB.\]
B.\[HI \bot AB.\]
C. \[\left( {SAB} \right) \bot \left( {SAC} \right).\]
D. \[\left( {SHI} \right) \bot \left( {SAB} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.Có đúng một mặt phẳng đi qua A và vuông góc với (P).
B.Có đúng hai mặt phẳng đi qua A và vuông góc với (P).
C.Có vô số mặt phẳng đi qua A và vuông góc với (P).
D.Không tồn tại mặt phẳng đi qua A và vuông góc với (P).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Ba mặt phẳng (ABC),(ABD),(ACD) đôi một vuông góc.
B.Hình chiếu của A lên mặt phẳng (BCD) là trực tâm của tam giác BCD.
C.Tam giác BCD vuông.
D. Hai cạnh đối của tứ diện vuông góc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.4
B.5
C.6
D.3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo