ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Hai mặt phẳng vuông góc
340 người thi tuần này 4.6 1.3 K lượt thi 19 câu hỏi 30 phút
🔥 Đề thi HOT:
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
13.6 K lượt thi
235 câu hỏi
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
18.8 K lượt thi
150 câu hỏi
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
4.9 K lượt thi
150 câu hỏi
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
17 K lượt thi
50 câu hỏi
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
5.1 K lượt thi
150 câu hỏi
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
3.8 K lượt thi
235 câu hỏi
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
14.2 K lượt thi
235 câu hỏi
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 4)
2.4 K lượt thi
235 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Gọi d là đường thẳng qua M và vuông góc với (P). Do\[\left( P \right)\,\,\parallel \,\,\left( Q \right) \Rightarrow d \bot \left( Q \right)\]
Giả sử (R) là mặt phẳng chứa d. Mà\(\left\{ {\begin{array}{*{20}{c}}{d \bot (P)}\\{d \bot (Q)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{(R) \bot (P)}\\{(R) \bot (Q)}\end{array}} \right.\)
Có vô số mặt phẳng (R) chứa d. Do đó có vô số mặt phẳng qua M, vuông góc với (P) và (Q).
Đáp án cần chọn là: D
Câu 2
A.Cho hai đường thẳng song song a và b và đường thẳng c sao cho \[c \bot a,\;\,c \bot b\]. Mọi mặt phẳng \[\left( \alpha \right)\] chứa c thì đều vuông góc với mặt phẳng (a,b).
B.Cho \[a \bot (\alpha ),\] mọi mặt phẳng \[\left( \beta \right)\;\]chứa a thì \[\left( \beta \right) \bot (\alpha ).\]
C.Cho \[a \bot b\], mọi mặt phẳng chứa b đều vuông góc với a.
D.Cho \[a \bot b\], nếu \[a \subset \left( \alpha \right)\] và\[b \subset \left( \beta \right)\] thì \[\left( \alpha \right) \bot (\beta ).\]
Lời giải
A sai. Trong trường hợp a,b, c đồng phẳng.
C sai. Trong trường hợp a và b cắt nhau, mặt phẳng (a,b) chứa b nhưng không vuông góc với a.
D sai. Trong trường hợp a và b vuông góc nhau và chéo nhau, nếu \[\left( \alpha \right) \supset a,\left( \alpha \right)\,\parallel \,b\] và \[\left( \beta \right) \supset b,\left( \beta \right)\,\parallel \,a\] thì \[\left( \alpha \right)\,\parallel \,\left( \beta \right)\]
Đáp án cần chọn là: B
Câu 3
A.Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B.Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
C.Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D.Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước
Lời giải
A sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau hoặc cắt nhau (giao tuyến vuông góc với mặt phẳng thứ 3).
B sai. Qua một đường thẳng chưa chắc đã có mặt phẳng vuông góc với một đường thẳng cho trước (vì nếu hai đường thẳng đã cho không vuông góc với nhau thì không có mặt phẳng nào hết)
D sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Đáp án cần chọn là: C
Câu 4
A. Ba mặt phẳng (ABC),(ABD),(ACD) đôi một vuông góc.
B.Hình chiếu của A lên mặt phẳng (BCD) là trực tâm của tam giác BCD.
C.Tam giác BCD vuông.
D. Hai cạnh đối của tứ diện vuông góc.
Lời giải
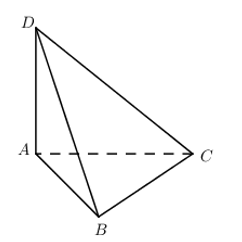
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{AD \bot AB}\\{AD \bot AC}\end{array}} \right. \Rightarrow AD \bot (ABC) \Rightarrow (ACD) \bot (ABC);(ABD) \bot (ABC)\\\left\{ {\begin{array}{*{20}{c}}{AC \bot AD}\\{AC \bot AB}\end{array}} \right. \Rightarrow AC \bot (ABD) \Rightarrow (ACD) \bot (ABD)\end{array}\)
⇒ A đúng.
\[AD \bot \left( {ABC} \right) \Rightarrow AD \bot BC\]Tương tự ta chứng minh được
\[AB \bot CD;\,\,AC \bot BD \Rightarrow D\]đúng.
Gọi H là trực tâm của tam giác BCD ta có
\(\left\{ {\begin{array}{*{20}{c}}{DH \bot BC}\\{AD \bot BC}\end{array}} \right. \Rightarrow BC \bot (ADH) \Rightarrow AH \bot BC\)
Tương tự ta chứng minh được\[AH \bot BD;\,\,AH \bot CD \Rightarrow AH \bot \left( {BCD} \right)\]⇒ B đúng.
Chưa đủ điều kiện để kết luận tam giác BCD vuông.
Đáp án cần chọn là: C
Lời giải
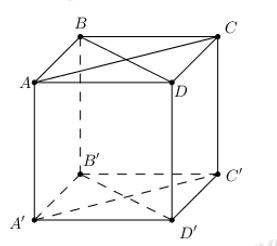
Có 6 hình bình hành thỏa mãn yêu cầu:\[ABB'A';\,\,BCC'B';\,\,CDD'C';\,\,ADD'A';\,\,ACC'A';\,\,BDD'B'\]
Đáp án cần chọn là: B
Câu 6
A.\[\left( {SAC} \right) \bot \left( {SAB} \right)\]
B. \[\left( {SAB} \right) \bot \left( {ABC} \right)\]
C. \[\left( {SAC} \right) \bot \left( {ABC} \right)\]
D. \[\left( {SAB} \right) \bot \left( {SBC} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[BM \bot AC.\]
B. \[\left( {SBM} \right) \bot \left( {SAC} \right).\]
C. \[\left( {SAB} \right) \bot \left( {SBC} \right).\]
D. \[\left( {SAB} \right) \bot \left( {SAC} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A.\[SH \bot AB.\]
B.\[HI \bot AB.\]
C. \[\left( {SAB} \right) \bot \left( {SAC} \right).\]
D. \[\left( {SHI} \right) \bot \left( {SAB} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A.\[BC \bot AH.\]
B. \[\left( {AHK} \right) \bot \left( {SBC} \right).\]
C. \[SC \bot AI.\]
D. Tam giác IAC đều
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A.\[SA \bot BH.\]
B. \[\left( {SDB} \right) \bot \left( {SDC} \right).\]
C. \[\left( {SAB} \right) \bot \left( {SAC} \right).\]
D. \[BH \bot HC.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A.tam giác.
B.hình thang cân.
C.hình thang vuông
D.hình bình hành
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A.tam giác đều
B.tam giác cân
C.tam giác vuông
D.tứ giác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A.\[S = \frac{{{a^2}}}{2}.\]
B. \[S = \frac{{{a^2}\sqrt 2 }}{2}.\]
C. \[S = \frac{{{a^2}\sqrt 3 }}{2}.\]
D. \[S = \frac{{{a^2}}}{4}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A.\[{S_{ABCD}} = {a^2}.\]
B. \[{S_{ABCD}} = \sqrt 2 \,{a^2}.\]
C. \[{S_{ABCD}} = \sqrt 3 \,{a^2}.\]
D. \[{S_{ABCD}} = 2\,{a^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A.\[{S_{{\rm{\Delta }}{\kern 1pt} ABC}} = \frac{{{a^2}\sqrt 2 }}{2}.\]
B. \[{S_{{\rm{\Delta }}{\kern 1pt} ABC}} = {a^2}\sqrt 2 .\]
C. \[{S_{{\rm{\Delta }}{\kern 1pt} ABC}} = \frac{{{a^2}\sqrt 2 }}{4}.\]
D. \[{S_{{\rm{\Delta }}{\kern 1pt} ABC}} = \frac{{{a^2}\sqrt 2 }}{6}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A.Có đúng một mặt phẳng đi qua A và vuông góc với (P).
B.Có đúng hai mặt phẳng đi qua A và vuông góc với (P).
C.Có vô số mặt phẳng đi qua A và vuông góc với (P).
D.Không tồn tại mặt phẳng đi qua A và vuông góc với (P).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A.4
B.5
C.6
D.3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
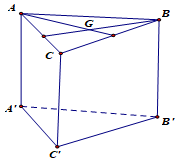
A.\[AG \bot B'C'\]
B. \[{\rm{AG}} \bot \left( {BCC'B'} \right)\]
C. \[{\rm{A}}{{\rm{A}}^\prime } \bot \left( {ABC} \right)\]
D. \[A'G \bot \left( {ABC} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo