Câu hỏi:
30/06/2022 143Trong không gian Oxyz, cho 3 điểm A(0;1;1),B(3;0;−1),C(0;21;−19) và mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\]. Điểm M thuộc mặt cầu (S) sao cho tổng \[3M{A^2} + 2M{B^2} + M{C^2}\;\] đạt giá trị nhỏ nhất, khi đó, độ dài vectơ \[\overrightarrow {OM} \;\] là
Đáp án chính xác
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
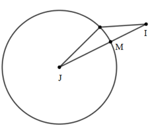
+) Mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\]có tâm J(1;1;1), bán kính R=1.
+) Tìm I: \[3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0 \Leftrightarrow 6\overrightarrow {IA} + 2\overrightarrow {AB} + \overrightarrow {AC} = \vec 0 \Leftrightarrow \overrightarrow {IA} = - \frac{{2\overrightarrow {AB} + \overrightarrow {AC} }}{6}\]
\[A\left( {0;1;1} \right),B\left( {3;0; - 1} \right),C\left( {0;21; - 19} \right)\]
\[ \Rightarrow \overrightarrow {IA} \left( { - {x_I};1 - {y_I};1 - {z_I}} \right),\overrightarrow {AB} \left( {3; - 1; - 2} \right),\overrightarrow {AC} \left( {0;20; - 20} \right)\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ - {x_I} = - \frac{{2.3 + 0}}{6}}\\{1 - {y_I} = - \frac{{2.( - 1) + 20}}{6}}\\{1 - {z_I} = - \frac{{2.( - 2) + ( - 20)}}{6}}\end{array}} \right. \Rightarrow I(1;4; - 3)\)
+) Ta có:
\[\begin{array}{*{20}{l}}{3M{A^2} + 2M{B^2} + M{C^2}}\\{ = 3{{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)}^2} + 2{{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)}^2} + {{\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)}^2}}\\{ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}}\\{ + 2.\overrightarrow {MI} .\left( {3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} } \right)}\\{ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\vec 0}\\{ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}}\end{array}\]
Để tổng trên là nhỏ nhất thì MI nhỏ nhất ⇒M là giao điểm của đoạn thẳng IJ và mặt cầu (S).
\[\overrightarrow {JI} = \left( {0;3; - 4} \right)\]=> Tọa độ điểm M thuộc đoạn IJ có dạng\[\left( {1;1 + 3t;1 - 4t} \right),t \in \left[ {0;1} \right]\]
Mặt khác\[M \in \left( S \right) \Rightarrow {\left( {1 - 1} \right)^2} + {\left( {1 - \left( {1 + 3t} \right)} \right)^2} + {\left( {1 - \left( {1 - 4t} \right)} \right)^2} = 1\]
\[ \Leftrightarrow {t^2} = \frac{1}{{25}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \frac{1}{5}}\\{t = - \frac{1}{5}\left( L \right)}\end{array}} \right. \Rightarrow t = \frac{1}{5} \Rightarrow M\left( {1;\frac{8}{5};\frac{1}{5}} \right) \Rightarrow OM = \frac{{3\sqrt {10} }}{5}\]
Đáp án cần chọn là: C
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;−2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.
Xem đáp án »
30/06/2022
4,569
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng \[\Delta :\frac{x}{1} = \frac{{y + 3}}{1} = \frac{z}{2}\;\]. Biết rằng mặt cầu (S) có bán kính bằng \(2\sqrt 2 \)và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính 2. Tìm tọa độ tâm I.
Xem đáp án »
30/06/2022
3,428
Câu 3:
Trong không gian với hệ tọa độ Oxyz. Hãy viết phương trình mặt cầu (S) có tâm I(2;0;1) và tiếp xúc với đường thẳng \[d:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z - 2}}{1}\].
Xem đáp án »
30/06/2022
2,837
Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình
\[{(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 50\]. Trong số các đường thẳng sau, mặt cầu (S) tiếp xúc với đường thẳng nào.
Xem đáp án »
30/06/2022
2,775
Câu 5:
Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu có điểm chung với trục Oz là:
Xem đáp án »
30/06/2022
956
Câu 6:
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(3;−2;0) và cắt trục Oy tại hai điểm A,B mà AB=8 là
Xem đáp án »
30/06/2022
455
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình \[{(x + 1)^2} + {(y - 1)^2} + {(z - 2)^2} = 4\]. Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua trục Oz.
Xem đáp án »
30/06/2022
313
về câu hỏi!