3 bài tập Đường tròn liên quan đến tứ giác nội tiếp đường tròn, chứng minh hệ thức, trung điểm, tỉ lệ cạnh (có lời giải)
72 người thi tuần này 4.6 139 lượt thi 3 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Lời giải
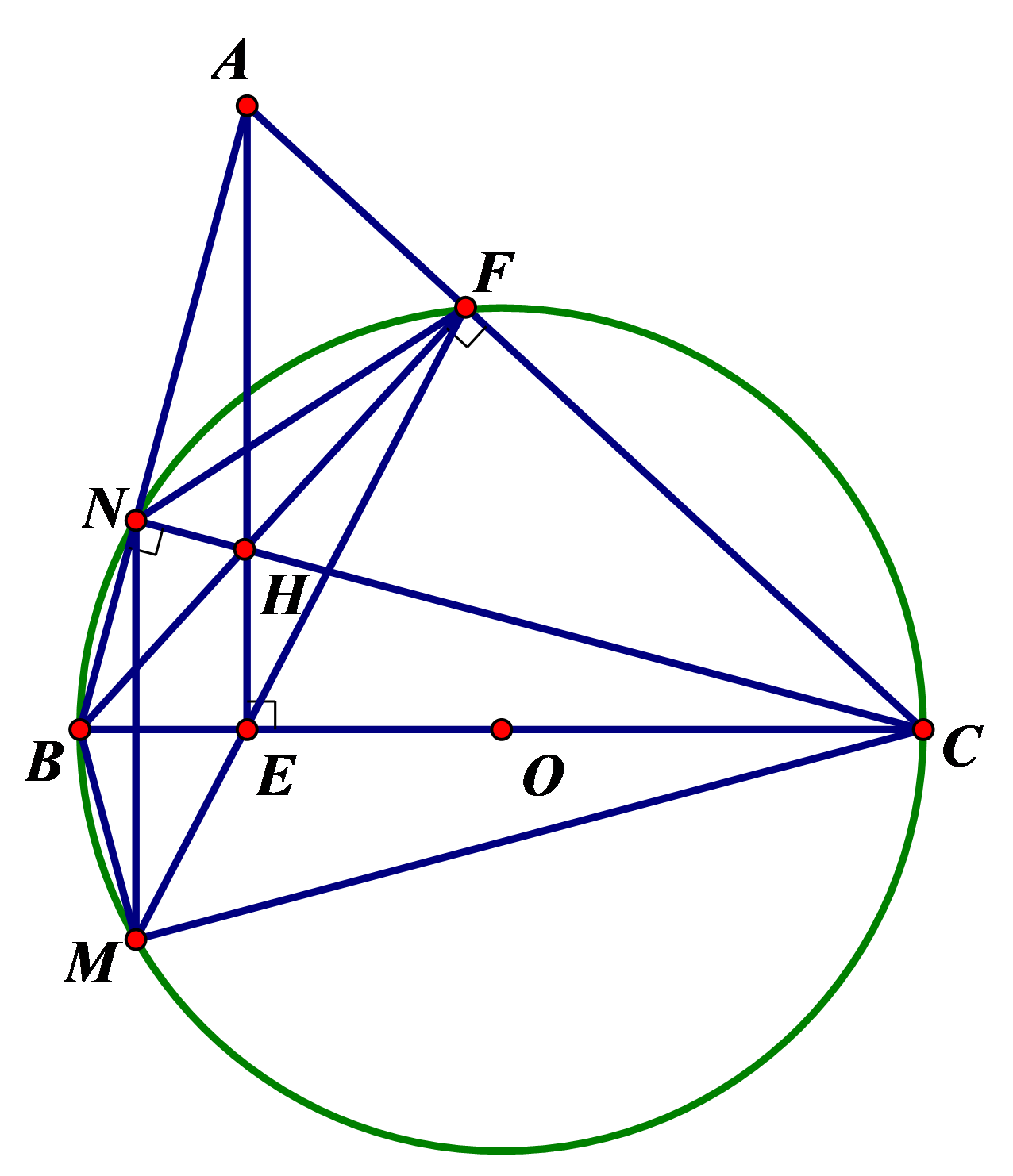
a) Chứng minh tứ giác \(CEHF\) nội tiếp.
Ta có:
\(HF \bot AC\left( {gt} \right) \Rightarrow \widehat {HFC} = 90^\circ \)
\(HE \bot BC\left( {gt} \right) \Rightarrow \widehat {HEC} = 90^\circ \)
Xét tứ giác \(CEHF\) có: \(\widehat {HFC} + \widehat {HEC} = 90^\circ + 90^\circ = 180^\circ \) mà hai góc này đối nhau
\( \Rightarrow CEHF\) là tứ giác nội tiếp.
b) Kéo dài \(FE\) cắt đường tròn đường kính \(BC\) tại \(M\). Chứng minh \(BM = BN\).
Ta có:
\(HN \bot AB\left( {gt} \right) \Rightarrow \widehat {ANH} = 90^\circ \)
\(HF \bot AC\left( {gt} \right) \Rightarrow \widehat {AFH} = 90^\circ \)
Xét tứ giác \(AFHN\) có: \(\widehat {ANH} + \widehat {AFH} = 90^\circ + 90^\circ = 180^\circ \) mà hai góc này đối nhau
\( \Rightarrow AFHN\) là tứ giác nội tiếp.
\( \Rightarrow \widehat {NAH} = \widehat {NFH}\) (2 góc nội tiếp cùng chắn cung \(HN\)) (1)
Tứ giác \(HECF\) nội tiếp (cmt)
\( \Rightarrow \widehat {HFE} = \widehat {HCE}\) (2 góc nội tiếp cùng chắn cung \(HE\)). (2)
Ta có: \(\widehat {BAE} = \widehat {NCB}\) (hai góc cùng phụ với \(\widehat {ABC}\)) \( \Rightarrow \widehat {NAH} = \widehat {HCE}\) (3)
Từ (1), (2), (3) suy ra \(\widehat {NFH} = \widehat {HFE}\) hay \(\widehat {NFB} = \widehat {BFM}\).
Xét \(\left( O \right)\) có: \(\widehat {NFB} = \widehat {BFM}\):
(hai góc nội tiếp bằng nhau hai cung chắn bằng nhau).
\( \Rightarrow BN = BM\) (hai cung chắn bằng nhau hai dây bằng nhau) (đpcm).
c) Biết \(AH = BC\). Tính số đo góc \(A\) của tam giác \(ABC\).
Xét hai tam giác vuông \(FAH\) và \(FBH\) ta có:
\(AH = BC\) (giả thiết)
\(\widehat {FAH} = \widehat {FBC}\) (vì cùng phụ với góc \(\widehat {ACE}\))
Vậy \(\Delta FAH = \Delta FBC\)
\( \Rightarrow FA = FB\)
Mặt khác tam giác \(AFB\) vuông có \(FA = FB\) nên nó vuông cân
Vậy \(\widehat {BAC} = {45^ \circ }\).
Lời giải
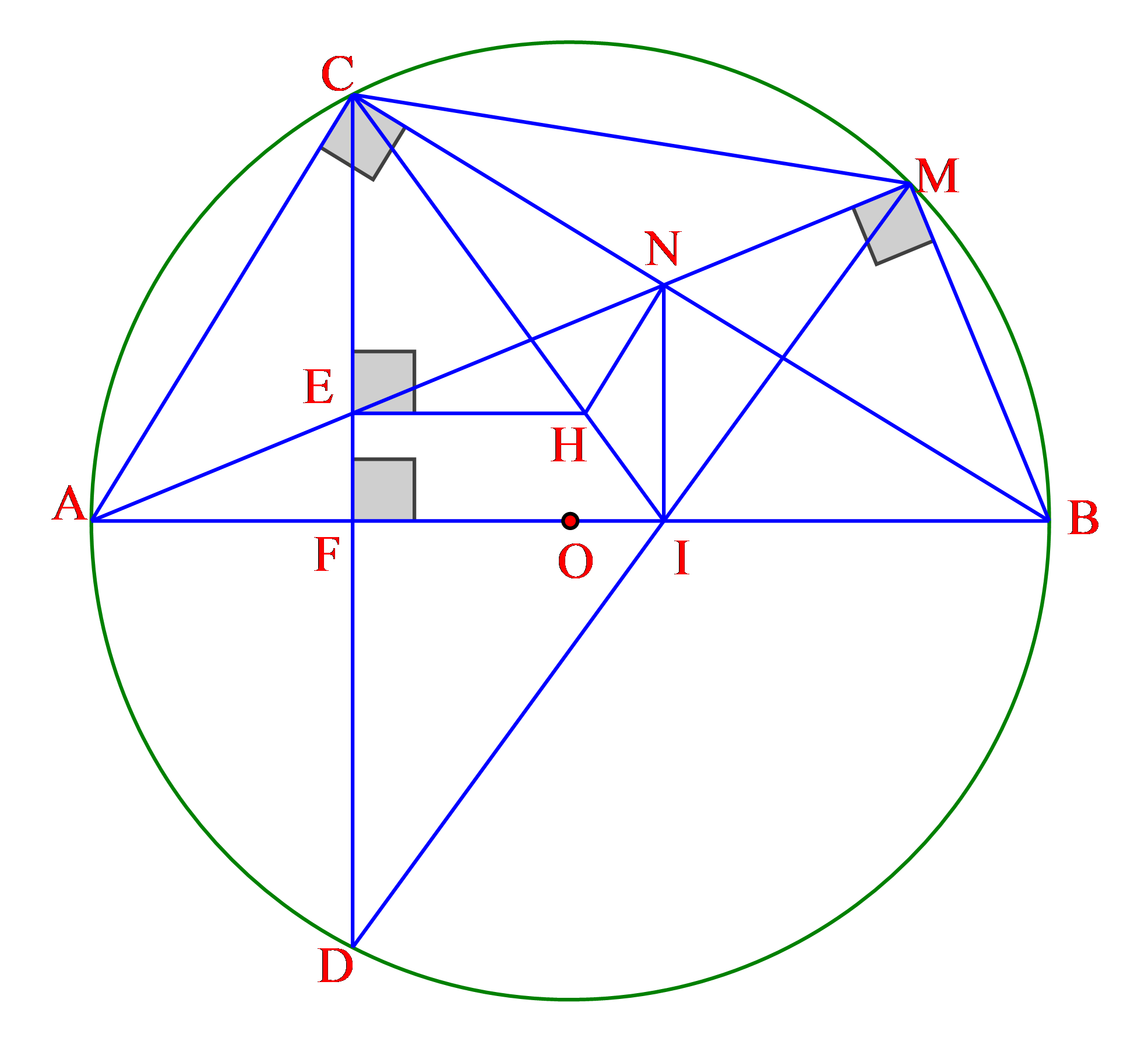
a)Xét tứ giác \(BMEF\) có:
\(\widehat {BFE\,} = {90^0}\) (gt)
\(\widehat {BFE\,} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \widehat {BFE\,} + \widehat {BME\,} = {180^0}\)
Mà hai góc \(\widehat {BFE\,},\,\,\widehat {BME\,}\) nằm ở vị trí đối nhau nên tứ giác \(BMEF\) nội tiếp
b) Ta có \(AB \bot CD \Rightarrow F\) là trung điểm của \(CD\)(mối liên hệ giữa đường kính và dây cung)
\( \Rightarrow AB\) là đường trung trực của \(CD\) \( \Rightarrow \)sđ = sđ
Ta có \(\widehat {AMC\,} = \frac{1}{2}\)sđ và \(\widehat {AMD\,} = \frac{1}{2}\)sđ
\( \Rightarrow \widehat {AMC\,} = \widehat {AMD\,} \Rightarrow AM\) là phân giác của \(\widehat {CMD\,}\)
c) Xét \(\Delta ACE\) và \(\Delta AMC\) có: \(\widehat {A\,\,}:\) chung
\(\widehat {AMC\,} = \frac{1}{2}\)sđ và \(\widehat {ACD\,} = \frac{1}{2}\)sđ\( \Rightarrow \widehat {AMC\,} = \widehat {ACD\,}\)
(g-g) \( \Rightarrow \frac{{AC}}{{AM}} = \frac{{AE}}{{AC}} \Rightarrow A{C^2} = AE.AM\)
d) Trên \(CI\) lấy điểm \(H\) sao cho \(HE\) vuông góc với \(CD\)
Cần chứng minh tứ giác \(CEHN\) nội tiếp đường tròn đường kính \(CH\), ta đi chứng minh \(\widehat {CNE\,} = \widehat {CHE\,}\)
Ta có: tứ giác \(BMNI\) nội tiếp
\( \Rightarrow \widehat {NIB\,} + \widehat {NMB\,} = {180^0} \Rightarrow \widehat {NIB\,} = {90^0} \Rightarrow \) tứ giác \(ACNI\) nội tiếp
Ta có: \(\widehat {CHE\,} = \widehat {CIA\,}\) (đồng vị); \(\widehat {CNE\,} = \widehat {CIA\,}\) (cùng chắn cung )
\( \Rightarrow \widehat {CNE\,} = \widehat {CHE\,} \Rightarrow \) tứ giác \(CEHN\) nội tiếp
Mà \(\widehat {CEH\,} = {90^0} \Rightarrow CH\) là đường kính
\( \Rightarrow \) tâm đường tròn ngoại tiếp tam giác \(CEN\) nằm trên \(CI\).
Lời giải
a) Chứng minh \[OM\] vuông góc với \[{O^'}M\].
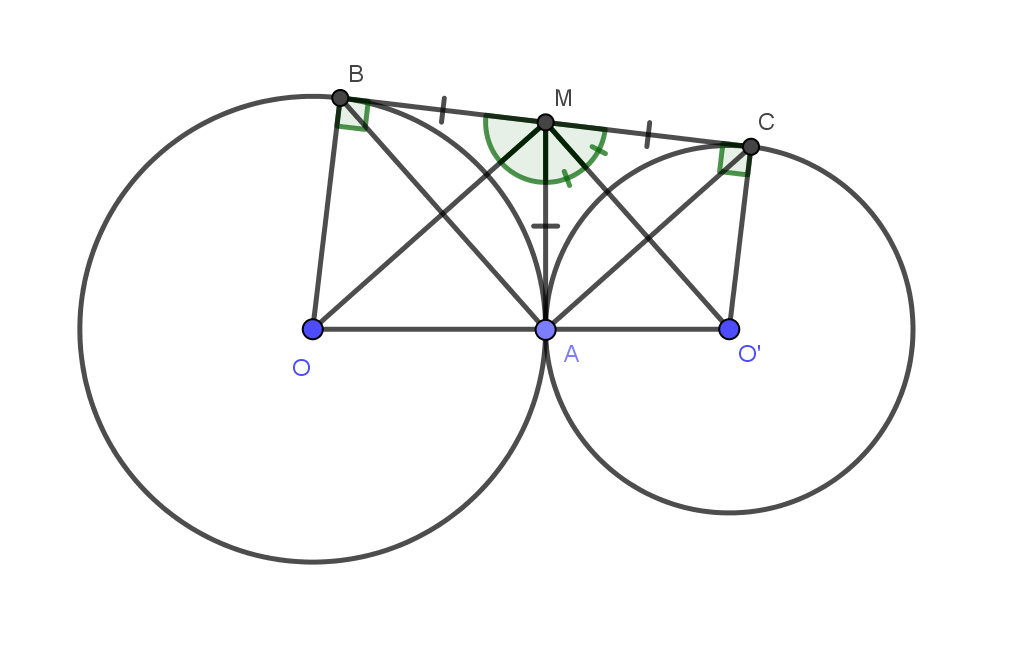
Vì \[MA\] và \[MB\] là tiếp tuyến của \[\left( O \right)\]nên \[MO\]
là tia phân giác của \[\widehat {AMB}\]. Do đó \[\widehat {OMA} = \frac{1}{2}\widehat {BMA}\]
\[MA\] và \[MC\] là tiếp tuyến của nên MO
là tia phân giác của \[\widehat {AMC}\]. Do đó
Suy ra
b) Gọi \[E\] là giao điểm của \[AB\] với \[OM\] và \[F\] là giao điểm của\[AC\]với O'M. Chứng minh tứ giác OEFO' nội tiếp một đường tròn.
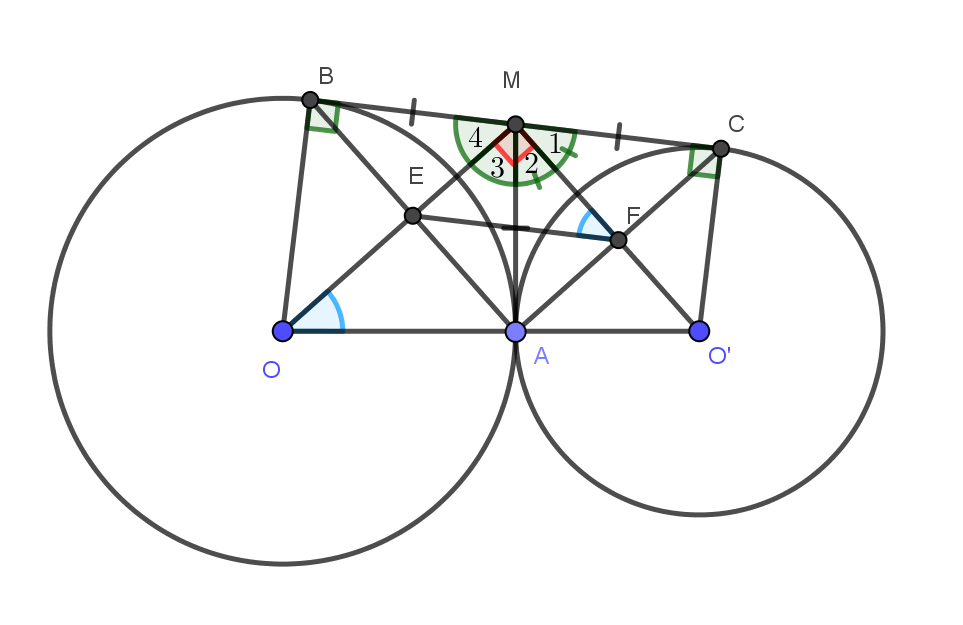
Ta có:
\[MB = MA\] ( tính chất của hai tiếp tuyến cắt nhau)
\[OB = OA\]( bán kính \[R\])
\[ \Rightarrow MO\] là đường trung trực của\[AB\]
\[ \Rightarrow MO \bot AB\] tại \[E \Rightarrow \widehat {MEA} = {90^0}\]
Tương tự, ta có: \[\widehat {MFA} = {90^0}\]
Xét tứ giác \[MEAF\] có:
\[ \Rightarrow \] tứ giác \[MEAF\]là hình chữ nhật ( theo dấu hiệu nhận biết)
\[ \Rightarrow MEAF\]là tứ giác nội tiếp
\[ \Rightarrow \widehat {MFE} = \widehat {MAE}\]
Trong tam giác vuông \[AOM\], ta có \[\widehat {MAE} = \widehat {OAE}\]
Vì vậy
Do đó, tứ giác OEFO' nội tiếp một đường tròn (góc ngoài bằng góc trong của đỉnh đối diện)
c) Gọi I là tâm đường tròn ngoại tiếp tứ giác OEFO', \[K\] là trung điểm của \[AM\]. Chứng minh
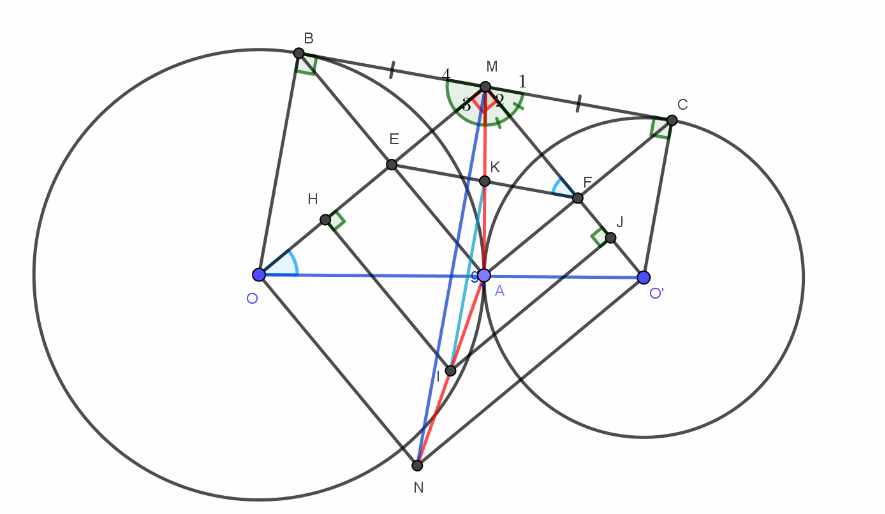
Cần xác định tâm \[I\] của đường tròn ngoại tiếp tứ giác OEFO'
Vẽ hai đường trung trực của hai đoạn thẳng \[EO\] và FO' lần lượt cắt \[EO\] và FO' tại \[H\]và \[J\]. Hai đường trung trực này cắt nhau tại \[I\]. \[I\] chính là tâm đường tròn ngoại tiếp tứ giác OEFO'
Qua \[O\] vẽ đường thẳng song song với MO'. Qua O' vẽ đường thẳng song song với\[MO\]. Hai đường thẳng này cắt nhau tại \[N\]. Theo cách vẽ ta được tứ giác MONO' là hình chữ nhật (vì có 3 góc vuông).
Suy ra OO' = MN (hai đường chéo của hình chữ nhật)
Chứng minh I là trung điểm của AN:
Hình thang \[AEON\]có \[HE = HO\]và \[HI\]//\[EA\]//\[ON\]
\[ \Rightarrow HI\] đi qua trung điểm của \[AN\] (1)
Tương tự, ta có \[JI\] đi qua trung điểm của \[AN\] (2)
Mà \[I = HI \cap JI\] (3)
Từ (1), (2) và (3) \[ \Rightarrow I\] là trung điểm của \[AN\]
Xét \[\Delta AMN\]có \[IK\]là đường trung bình của tam giác