Bài tập chuyên đề Toán 7 Dạng 7: Các trường hợp bằng nhau của tam giác vuông có đáp án

Thi Online Bài tập chuyên đề Toán 7 Dạng 7: Các trường hợp bằng nhau của tam giác vuông có đáp án

Đề số 1

Bài tập chuyên đề Toán 7 Dạng 7: Các trường hợp bằng nhau của tam giác vuông có đáp án

238 lượt thi
19 câu hỏi
50 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Cho tam giác cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D. Chứng minh rằng AD là tia phân giác của góc BAC.

Xem đáp án

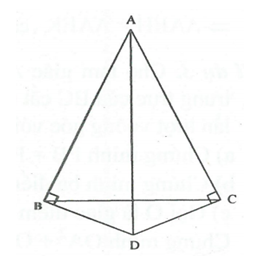
Cho tam giác cân tại A. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D. (ảnh 1)

* Tìm cách giải. Để chứng minh AD là tia phân giác của góc BAC, chúng ta cần chứng minh $\hat{B A D} = \hat{C A D}$ . Do đó hiển nhiên cần chứng minh $Δ B A D = Δ C A D$

* Trình bày lời giải.

Xét $Δ B A D$ và $Δ C A D$ có: $\hat{A B D} = \hat{A C D} (= 90 °)$ ; AD là cạnh chung; $A B = A C$ ( $Δ A B C$ cân tại A).

Do đó $Δ B A D = Δ C A D$ (cạnh huyền - cạnh góc vuông)

$\Rightarrow \hat{B A D} = \hat{C A D}$ (cặp góc tương ứng).

Vậy AD là tia phân giác góc BAC.

* Nhận xét. Chúng ta còn có DA là tia phân giác của góc BDC, tam giác DBC cân tại D.

AD vuông góc với BC.

Câu 2:

Cho tam giác ABC vuông tại A, vẽ AH vuông góc với BC. Trên cạnh BC lấy điểm E sao cho BA=BE. Kẻ $E K ⊥ A C (K \in A C)$ . Chứng minh rằng $A K = A H .$

Xem đáp án

* Tìm cách giải. Để chứng minh AK= AH, chúng ta cần ghép chúng vào hai tam giác và chứng minh hai tam giác đó bằng nhau. Do vậy cần chứng minh

Δ A E H = Δ A E K

.
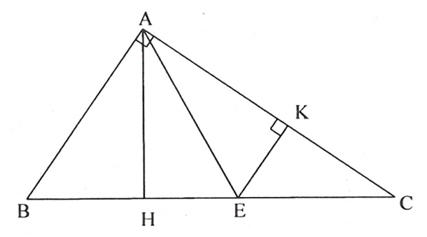
* Trình bày lời giải.

Δ A B E

cân tại B nên

\hat{B A E} = \hat{B E A}, E K / / A B

(vì cùng vuông góc với AC)

\Rightarrow \hat{E A B} = \hat{A E K}

(slt)

\Rightarrow \hat{A E H} = \hat{A E K}

\Rightarrow Δ A E H = Δ A E K

(ch- gn )

\Rightarrow A K = A H

Câu 3:

Cho tam giác ABC (AB < AC), M là trung điểm của BC. Đường trung trực của BC cắt tia phân giác của góc BAC tại điểm P. Vẽ PH và PK lần lượt vuông góc với đường thẳng AB và đường thẳng AC.

a) Chứng minh PB = PC và BH = CK.

Xem đáp án

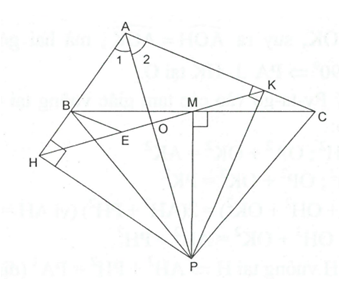
Cho tam giác ABC (AB < AC), M là trung điểm của BC. Đường trung trực của BC cắt tia phân giác của góc BAC tại điểm P. (ảnh 1)

a) $Δ P M B$ và $Δ P M C$ có

$\hat{P M B} = \hat{P M C} (= 90 °), M B = M C$ , MP là cạnh chung

$\Rightarrow Δ P M B = Δ P M C (c . g . c) \Rightarrow P B = P C$ (hai cạnh tương ứng)

Câu 4:

b) Chứng minh ba điểm H, M, K thẳng hàng.

Xem đáp án

b) $Δ P H A$ và $Δ P K A$ có $\hat{P H A} = \hat{P K A} (= 90 °), \hat{P A H} = \hat{P A K}$ , AP là cạnh chung

$\Rightarrow Δ P H A = Δ P K A$ (cạnh huyền - góc nhọn)

$\Rightarrow P H = P K$ (hai cạnh tương ứng)

$Δ P H B$ và $Δ P K C$ có $\hat{P H B} = \hat{P K C} = 90 °, P B = P C, P H = P K$

$\Rightarrow Δ P H B = Δ P K C$ (cạnh huyền - cạnh góc vuông)

$\Rightarrow B H = C K$ (hai cạnh tương ứng)

Câu 5:

c) Gọi O là giao điểm của PA và HK.

Chứng minh $O A^{2} + O P^{2} + O H^{2} + O K^{2} = P A^{2}$

Xem đáp án

c) $Δ A O H$ và $Δ A O K$ có $A H = A K, \hat{O A H} = \hat{O A K}, A O$ là cạnh chung

$\Rightarrow Δ A O H = Δ A O K$ , suy ra $\hat{A O H} = \hat{A O K}$ , mà hai góc này kề bù nên

$\hat{A O H} = \hat{A O K} = 90 ° \Rightarrow P A ⊥ H K$ tại O.

Áp dụng định lý Py-ta-go vào các tam giác vuông tại O là OAH, OAK, OPH, OPK ta có:

$O A^{2} + O H^{2} = A H^{2}; O A^{2} + O K^{2} = A K^{2}$

$O P^{2} + O H^{2} = P H^{2}; O P^{2} + O K^{2} = P K^{2}$

$\Rightarrow 2 (O A^{2} + O P^{2} + O H^{2} + O K^{2}) = 2 (A H^{2} + P H^{2})$ (vì $A H = A K$ và $P H = P K$ )

$\Rightarrow O A^{2} + O P^{2} + O H^{2} + O K^{2} = A H^{2} + P H^{2}$

Mà tam giác PAH vuông tại H $\Rightarrow A H^{2} + P H^{2} = P A^{2}$ (định lý Py-ta-go)

$\Rightarrow O A^{2} + O P^{2} + O H^{2} + O K^{2} = P A^{2}$

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Các bài thi hot trong chương

Đánh giá trung bình

Thi Online Bài tập chuyên đề Toán 7 Dạng 7: Các trường hợp bằng nhau của tam giác vuông có đáp án