Đề kiểm tra Đường thẳng và mặt phẳng trong không gian (có lời giải) - Đề 3
29 người thi tuần này 4.6 608 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Chọn C
![Chọn C \[\left\{ \begin{array}{l}I \in AD \subset \left( {KAD} \right)\\I \in \left( {IBC} \right)\end{array} \right.\] \[ \Rightarrow I\] là điểm chung t (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/20-1759680157.png)
\[\left\{ \begin{array}{l}I \in AD \subset \left( {KAD} \right)\\I \in \left( {IBC} \right)\end{array} \right.\] \[ \Rightarrow I\] là điểm chung thứ nhất của hai mặt phẳng \[\left( {IBC} \right)\] và \[\left( {KAD} \right)\].
\[\left\{ \begin{array}{l}K \in BC \subset \left( {IBC} \right)\\K \in \left( {KAD} \right)\end{array} \right.\]\[ \Rightarrow K\] là điểm chung thứ hai của hai mặt phẳng \[\left( {IBC} \right)\] và \[\left( {KAD} \right)\].
Vậy \[\left( {IBC} \right) \cap \left( {KAD} \right) = IK\].
Câu 2
Lời giải
Chọn D
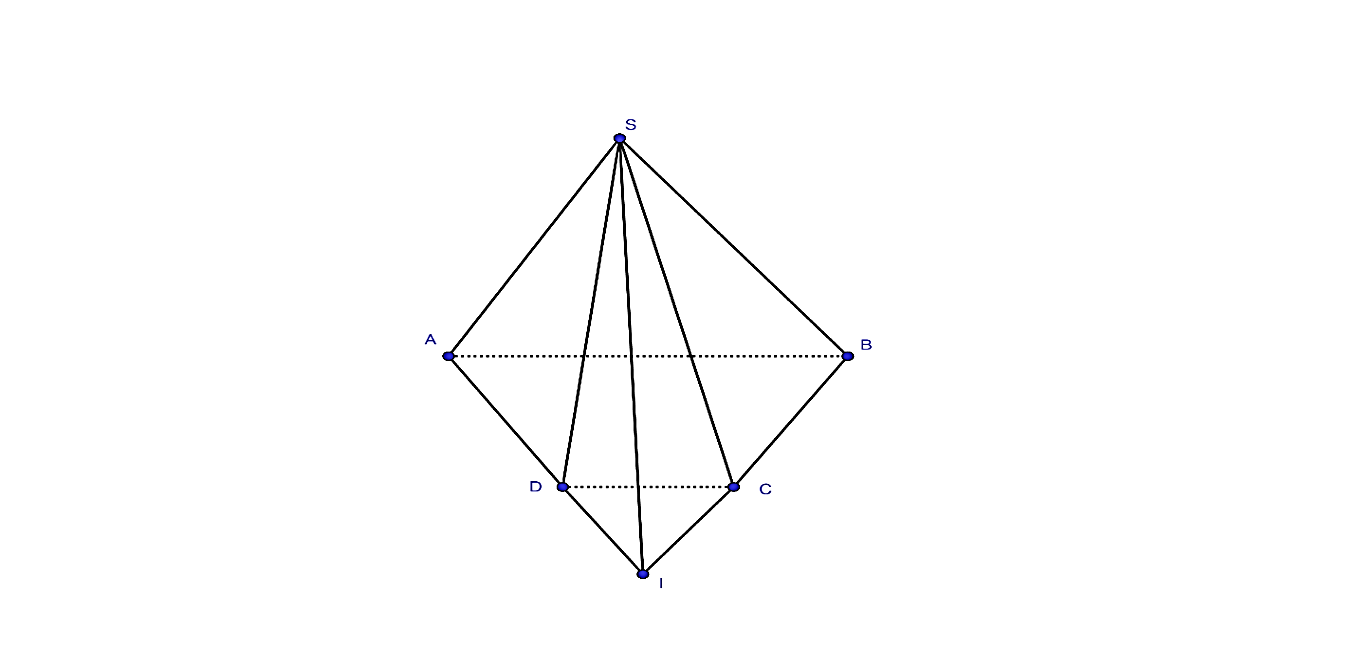
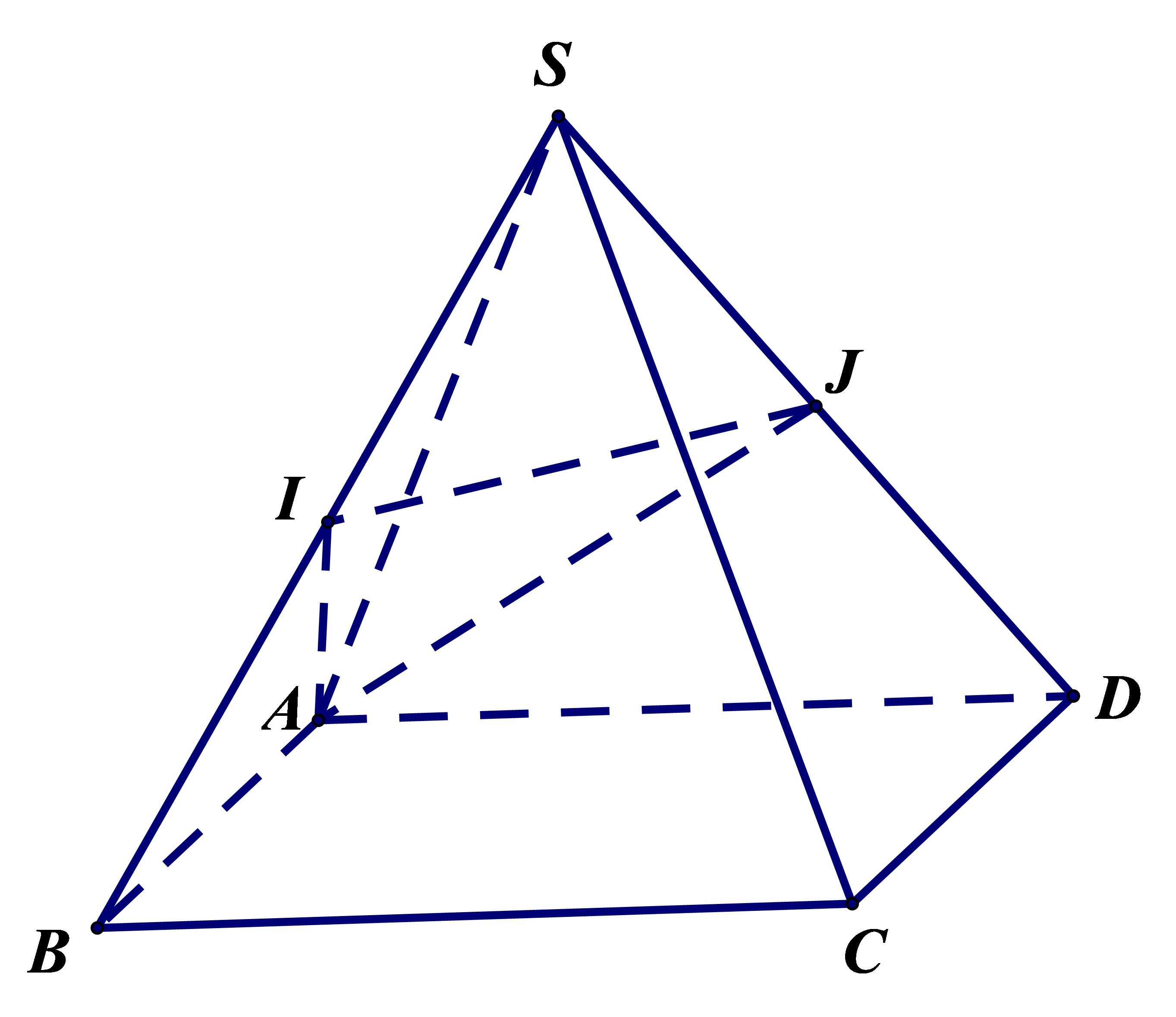
Ta có: \(S \in \left( {SAD} \right) \cap \left( {SBC} \right)\)
Trong \(mp\left( {ABCD} \right)\), gọi \(I = AD \cap BC \Rightarrow I \in \left( {SAD} \right) \cap \left( {SBC} \right)\)
Vậy \(SI = \left( {SAD} \right) \cap \left( {SBC} \right)\).
Câu 3
Lời giải
Chọn B
![Chọn B Gọi giao điểm của \[BG\] với \[CD\] là \[N\], ta thấy hai mặt phẳng \[\left( {ACD} \right)\] và \[\left( {GAB} \right)\] có hai điểm chung là \[A\] và \[N\] nên giao tuyến của chúng là \[AN\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/2-1759681307.png)
Gọi giao điểm của \[BG\] với \[CD\] là \[N\], ta thấy hai mặt phẳng \[\left( {ACD} \right)\] và \[\left( {GAB} \right)\] có hai điểm chung là \[A\] và \[N\] nên giao tuyến của chúng là \[AN\].
Câu 4
Lời giải
Chọn A
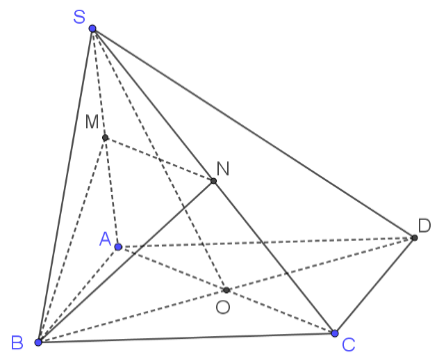
![Chọn A Gọi \[O\] là tâm của hình bình hành \[ABCD\]. Trong mặt phẳng \[\left( {SAC} \right)\], gọi \(I\) là giao điểm của \[AM\]và\[SO\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/3-1759681373.png)
Gọi \[O\] là tâm của hình bình hành \[ABCD\]. Trong mặt phẳng \[\left( {SAC} \right)\], gọi \(I\) là giao điểm của \[AM\]và\[SO\]. Khi đó \(I\) là trọng tâm tam giác \(SAC\). Vậy \(\overrightarrow {IA} = - \,2\overrightarrow {IM} \).
Câu 5
Lời giải
Chọn A
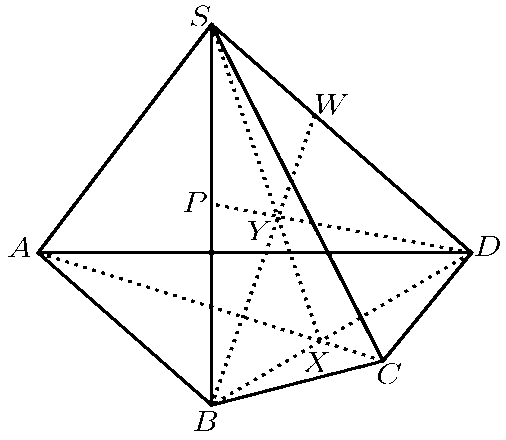
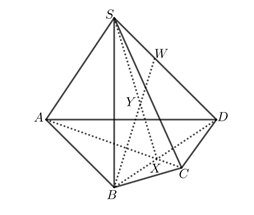
Trong mặt phẳng \(\left( {SBD} \right)\) gọi \(P\) là giao điểm của \(DY\) và \(SB\).
Ta có: \(\left\{ \begin{array}{l}P \in DY\\P \in SB \subset \left( {SAB} \right) \Rightarrow P \in \left( {SAB} \right)\end{array} \right.\). Vậy \(P\) là giao điểm của \(DY\) với \(\left( {SAB} \right)\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.