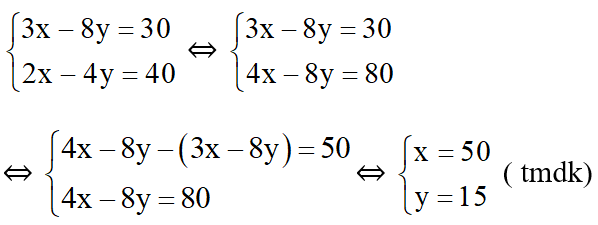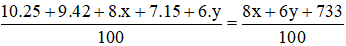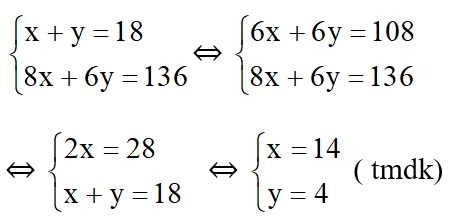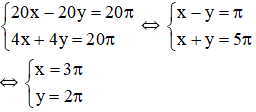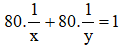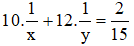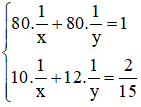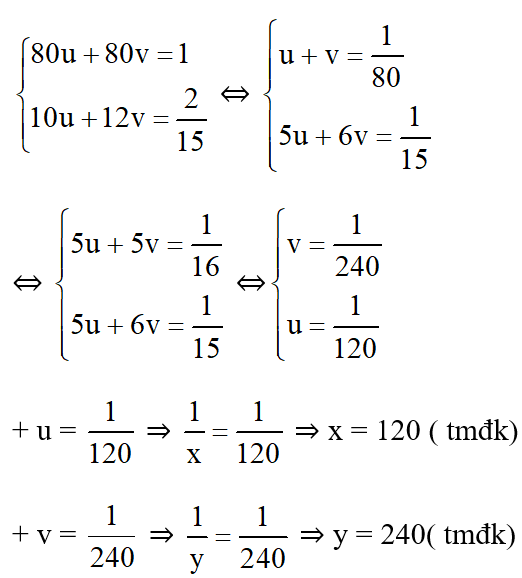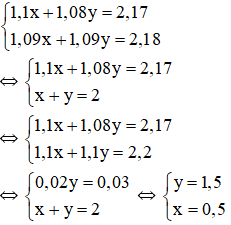Giải bài tập SGK Toán 9 tập 2 hay nhất Luyện tập (trang 24-25 sgk)
35 người thi tuần này 4.6 2.3 K lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Gọi x là số luống rau, y là số cây mỗi luống.
Điều kiện x > 4, y > 3; x,y ∈ N
Số cây trong vườn là: x.y (cây)
+ Tăng 8 luống, mỗi luống ít hơn 3 cây thì số luống là x + 8, số cây mỗi luống là y – 3
⇒ Tổng số cây trong vườn là (x + 8)(y – 3) cây.
Số cây trong vườn ít đi 54 cây nên ta có phương trình:
(x + 8)(y – 3) = xy – 54
⇔ xy -3x + 8y - 24 = xy – 54
⇔ xy -3x + 8y - xy = –54 + 24
⇔ -3x + 8y = –30
⇔ 3x – 8y = 30
+ Giảm 4 luống mỗi luống tăng thêm 2 cây thì số luống là x – 4 và số cây mỗi luống là y + 2.
⇒ Số cây trong vườn là: (x – 4)(y + 2) cây
Số cây trong vườn tăng thêm 32 cây nên ta có phương trình:
(x – 4)(y + 2) = xy + 32
⇔ xy – 4y + 2x – 8 = xy + 32
⇔ 2x – 4y = 40
Ta có hệ phương trình:
Vậy số rau cải bắp nhà Lan trồng là : 15.50 = 750 cây.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Lời giải
Gọi số lần bắn đạt điểm 8 là x, số lần bắn đạt điểm 6 là y.
Điều kiện x, y ∈ N; x < 18, y < 18.
Tổng số lần bắn là 100 nên ta có: 25 + 42 + x + 15 + y = 100 ⇔ x + y = 18.
Điểm trung bình là :
Điểm trung bình bằng 8,69 nên ta có phương trình :
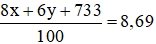
Ta có hệ phương trình :
Vậy số lần bắn đạt 8 điểm là 14 và số lần bắn đạt 6 điểm là 4.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Lời giải
Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s)
Điều kiện x , y > 0.
Chu vi vòng tròn là : 20.π (cm)
Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây chênh lệch nhau đúng bằng 1 vòng tròn
⇒ Ta có phương trình: 20x – 20y = 20π.
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đường hai vật đi được trong 4 giây là đúng 1 vòng tròn
⇒ Ta có phương trình: 4x + 4y = 20π.
Ta có hệ phương trình:
Vậy vận tốc của hai vật là 3π cm/s, 2π cm/s.
Chú ý : Chu vi đường tròn bán kính R là : P= 2πR= πd trong đó d là đường kính của đường tròn.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Lời giải
Gọi x (phút), y (phút) lần lượt là thời gian vòi thứ nhất, vòi thứ hai chảy một mình để đầy bể.
(Điều kiện: x, y > 80 )
Trong 1 phút vòi thứ nhất chảy được 1/x bể; vòi thứ hai chảy được 1/y bể.
Sau 1 giờ 20 phút = 80 phút, cả hai vòi cùng chảy thì đầy bể nên ta có phương trình:
Mở vòi thứ nhất trong 10 phút và vòi thứ 2 trong 12 phút thì chỉ được 2/15 bể nước nên ta có phương trình :
Ta có hệ phương trình:
Đặt 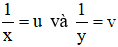
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (= 2 giờ) , vòi thứ hai 240 phút (= 4 giờ)
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Lời giải
Giả sử giá của loại hàng thứ nhất và thứ hai không tính VAT lần lượt là x, y
(x, y > 0, triệu đồng; x < 2,17, y < 2,17)
Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x
+ Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.
Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình: 1,1x + 1,08y = 2,17 (1)
Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x
+ Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.
Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:
1,09x + 1,09y = 2,18 ⇔ x+ y = 2 (2)
Từ (1) và (2) ta có hệ phương trình :
Vậy: nếu không kể thuế VAT thì người đó phải trả : 0,5 triệu cho loại thứ nhất và 1,5 triệu cho loại thứ hai .
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.