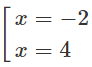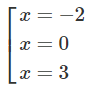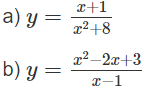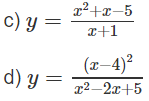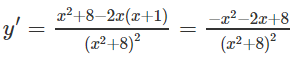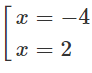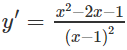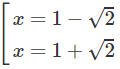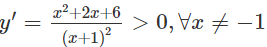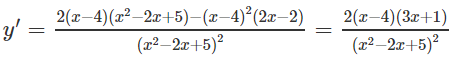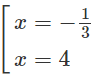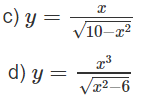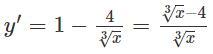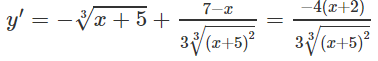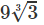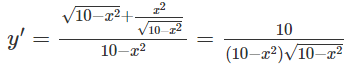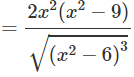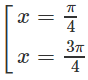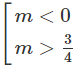Giải sbt Giải tích 12 Bài 2: Cực trị của hàm số
28 người thi tuần này 4.6 2.6 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a) y = −2 + 7x − 5. TXĐ: R
y′ = −4x + 7, y′ = 0 ⇔ x = 7/4
y′′ = −4 ⇒ y′′(7/4) = −4 < 0
Vậy x = 7/4 là điểm cực đại của hàm số và = 9/8
b) y = . TXĐ: R
=
y′ = 0 ⇔
Vì y′′(−2) = −18 < 0, y′′(4) = 18 > 0 nên hàm số đạt cực đại tại x = -2; đạt cực tiểu tại x = 4 và = y(-2) = 35; = y(4) = -73.
e) TXĐ: R
y′ = 2(x + 2). + 3. = 5x(x + 2).
y′= 0 ⇔
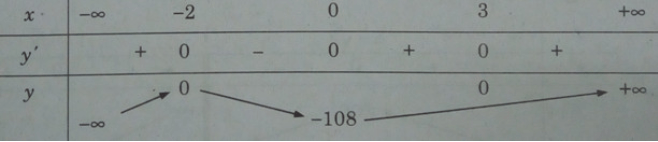
Bảng biến thiên:
Từ đó suy ra = y(-2) = 0; = y(0) = -108.
Lời giải
a) TXĐ : R
y′= 0 ⇔
Bảng biến thiên:
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = -4 và = y(2) = 1/4; = y(−4) = −1/8
b) Hàm số xác định và có đạo hàm với mọi x ≠ 1.
y′=0 ⇔
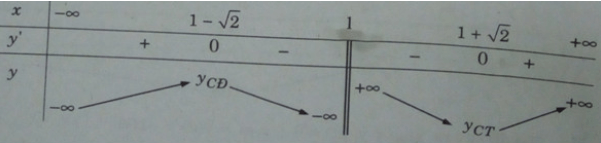
Bảng biến thiên:
Hàm số đạt cực đại tại x = 1 − và đạt cực tiểu tại x = 1 + , ta có:
yCD = y(1 − ) = −2;
yCT = y(1 + ) = 2.
c) TXĐ: R\{-1}
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
d) Vì – 2x + 5 luôn luôn dương nên hàm số xác định trên ()
y′ = 0 ⇔
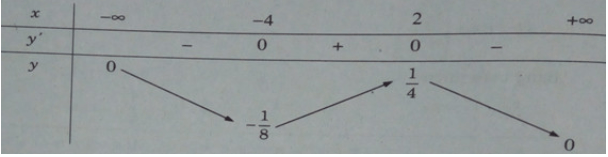
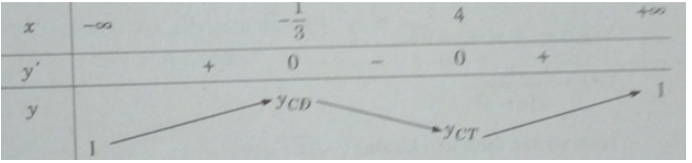
Bảng biến thiên:
Hàm số đạt cực đại tại x = −1/3, đạt cực tiểu tại x = 4 và = y(−1/3) = 13/4; = y(4) = 0
Lời giải
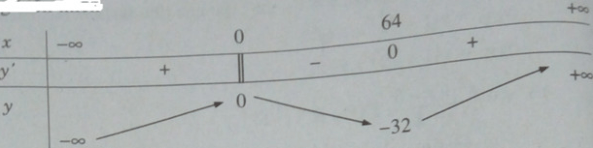
a) TXĐ: R
y′ = 0 ⇔ x = 64
Bảng biến thiên:
Vậy ta có = y(0) = 0 và = y(64) = -32.
b) Hàm số xác định trên khoảng ().
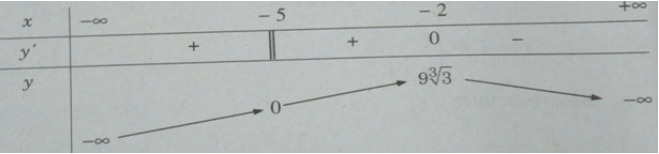
Bảng biến thiên:
Vậy = y(−2) =
c) Hàm số xác định trên khoảng (−;).
Vì y’ > 0 với mọi (−;) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
d) TXĐ: D = (−; −) ∪ (; +)
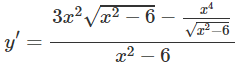
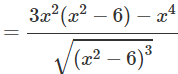
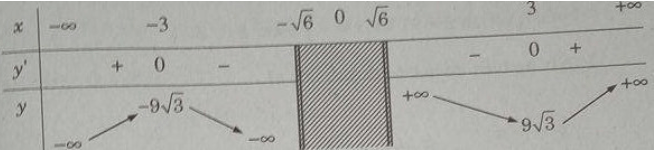
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = -3 và = y(3) = 9; = y(−3) = −9
Lời giải
a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔
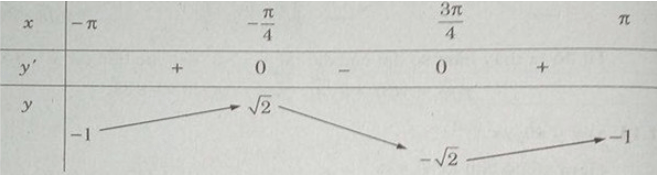
Bảng biến thiên:
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và = y(π/4) = 1; = y(3π/4) = −1
Vậy trên R ta có:
= y(π/4 + kπ) = 1;
= y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
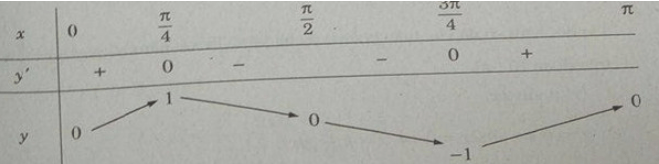
Lập bảng biến thiên trên đoạn [−π;π]
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
= y(−π4 + k2π) = ;
= y(3π4 + k2π) = − (k∈Z).
c) Ta có:
![]()
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
![]()
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
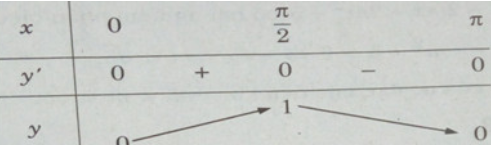
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
= y(2mπ) = 0; yCT = y(2mπ) = 0;
= y((2m+1)π/2) = 1 (m∈Z)
Lời giải
TXĐ: D = R
y’ = 3 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3 + 4mx + m có hai nghiệm phân biệt.
⇔ Δ’ = 4 -3m > 0 ⇔ m(4m – 3) > 0
⇔
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.