Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường \[y = {x^2} + 1;x = 0\] và tiếp tuyến của đồ thị hàm số \[y = {x^2} + 1\;\] tại điểm A(1;2) quanh trục Ox là
A.\[\frac{2}{5}\pi \]
B. \(\pi \)
C. \[\frac{1}{2}\pi \]
D. \[\frac{8}{{15}}\pi \]
Quảng cáo
Trả lời:
\[y' = 2x;y'\left( 1 \right) = 2\] suy ra phương trình tiếp tuyến là\[y = 2\left( {x - 1} \right) + 2 = 2x\]
Ta có: \[{x^2} + 1 = 2x \Leftrightarrow x = 1\]
Trong đoạn\[[0;1]\] thì \[{x^2} + 1 \ge 2x\] nên:
Thể tích khối tròn xoay
\[V = \pi \mathop \smallint \limits_0^1 \left[ {{{\left( {{x^2} + 1} \right)}^2} - {{\left( {2x} \right)}^2}} \right]dx = \pi \mathop \smallint \limits_0^1 \left( {{x^4} - 2{{\rm{x}}^2} + 1} \right)dx = \frac{8}{{15}}\pi \]
Đáp án cần chọn là: D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\[a = 2\sqrt 2 \]
B. \[a = \frac{5}{2}\]
C. \[a = 2\]
D. \[a = 3\]
Lời giải
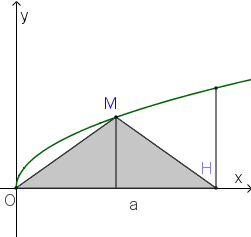
Gọi V1 là thể tích khối tròn tạo thành khi quay quanh tam giác OMH quanh trục Ox. Biết rằng \[V = 2{V_{1\;}}\]. Khi đó:
Thể tích khối tròn xoay\(V = \pi \int\limits_0^4 {xdx = \pi \frac{{{x^2}}}{2}} \left| {_0^4} \right. = 8\pi \)
Suy ra\[{V_1} = 4\pi \]
Gọi N là giao điểm của đường thẳng x=a và trục hoành. Khi đó V1 là thể tích tạo được khi xoay hai tam giác OMN và MNH quanh trục Ox với N là hình chiếu của M trên OH.
Ta có \[{V_1} = \frac{1}{3}\pi .a.{\left( {\sqrt a } \right)^2} + \frac{1}{3}\pi .\left( {4 - a} \right).{\left( {\sqrt a } \right)^2} = \frac{4}{3}\pi a\]
Suy ra\[\frac{4}{3}\pi a = 4\pi \Rightarrow a = 3\]
Đáp án cần chọn là: D
Câu 2
A.\[V = \pi \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\]
B. \[V = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\]
C. \[V = \pi \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\]
D. \[V = {\pi ^2}\mathop \smallint \limits_a^b {f^2}\left( x \right)dx\]
Lời giải
Thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số\[y = f\left( x \right)\] trục Ox và hai đường thẳng\[x = a,x = b(a < b)\] quanh trục Ox là: \[V = \pi \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\]
Đáp án cần chọn là: C
Câu 3
A.\[V = \pi \mathop \smallint \limits_0^2 (2 - x)dx + \pi \mathop \smallint \limits_0^2 {x^2}dx\]
B. \[V = \pi \mathop \smallint \limits_0^2 (2 - x)dx\]
C. \[V = \pi \mathop \smallint \limits_0^1 xdx + \pi \mathop \smallint \limits_1^2 \sqrt {2 - x} dx\]
D. \[V = \pi \mathop \smallint \limits_0^1 {x^2}dx + \pi \mathop \smallint \limits_1^2 (2 - x)dx\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\[a \in \left( {\frac{1}{2};1} \right).\]
B.\[a \in \left( {1;\frac{3}{2}} \right).\]
C. \[a \in \left( {\frac{3}{2};2} \right).\]
D. \[a \in \left( {2;\frac{5}{2}} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[V = 36\pi .\]
B. \[V = 24\pi .\]
C. \[V = 16\pi .\]
D. \[V = 64\pi .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[V = 32 + 2\sqrt {15} \]
B. \[V = \frac{{124\pi }}{3}\]
C. \[V = \frac{{124}}{3}\]
D. \[V = (32 + 2\sqrt {15} )\pi \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[V = 4 - 2e\]
B. \[V = \left( {4 - 2e} \right)\pi \]
C. \[V = {e^2} - 5\]
D. \[V = \left( {{e^2} - 5} \right)\pi \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.