4 bài tập Tính bán kính đáy, đường cao, diện tích, thể tích của hình nón (có lời giải)
40 người thi tuần này 4.6 80 lượt thi 4 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Lời giải
· Với \[r = 3,h = 4\]
Đường sinh của hình nón: \[l = \sqrt {{r^2} + {h^2}} = \sqrt {{3^2} + {4^2}} = 5\]
Diện tích xung quanh: \[{S_{xq}} = \pi rl = 15\pi \left( {c{m^2}} \right)\]
Diện tích toàn phần: \[{S_{tp}} = \pi r\left( {l + r} \right) = 24\pi \left( {c{m^2}} \right)\]
Thể tích: \[V = \frac{1}{3}\pi {r^2}h = 12\pi \left( {c{m^2}} \right)\]
· Với \[h = 4,l = 10\]
Bán kính của hình nón: \[r = \sqrt {{l^2} - {h^2}} = \sqrt {{{10}^2} - {8^2}} = 6\]
Diện tích xung quanh: \[{S_{xq}} = \pi rl = 60\pi \left( {c{m^2}} \right)\]
Diện tích toàn phần: \[{S_{tp}} = \pi r\left( {l + r} \right) = 64\pi \left( {c{m^2}} \right)\]
Thể tích: \[V = \frac{1}{3}\pi {r^2}h = \frac{{144}}{3}\pi \left( {c{m^2}} \right)\]
· Với \[r = 2,{S_{xq}} = 14\pi \]
Đường sinh của hình nón: \[{S_{xq}} = \pi rl \Rightarrow l = \frac{{{S_{xq}}}}{{\pi r}} = \frac{{14\pi }}{{2\pi }} = 7cm\]
Chiều cao của hình nón: \[h = \sqrt {{l^2} - {r^2}} = \sqrt {{7^2} - {2^2}} = 3\sqrt 5 cm\]
Diện tích toàn phần: \[{S_{tp}} = \pi r\left( {l + r} \right) = 18\pi \left( {c{m^2}} \right)\]
Thể tích: \[V = \frac{1}{3}\pi {r^2}h = 4\sqrt 5 \pi \left( {c{m^2}} \right)\]
· Với \[r = 4,l = 9\]
Chiều cao của hình nón: \[h = \sqrt {{l^2} - {r^2}} = \sqrt {81 - 16} = \sqrt {65} cm\]
Diện tích xung quanh: \[{S_{xq}} = \pi rl = 36\pi \left( {c{m^2}} \right)\]
Diện tích toàn phần: \[{S_{tp}} = \pi r\left( {l + r} \right) = 42\pi \left( {c{m^2}} \right)\]
Thể tích: \[V = \frac{1}{3}\pi {r^2}h = \frac{{16\sqrt {65} \pi }}{3}\left( {c{m^2}} \right)\]
Lời giải
Gọi \(r,h\) lần lượt là bán kính đường tròn đáy và chiều cao của hình nón ban đầu.
Thể tích hình nón ban đầu là \[{V_1} = \frac{1}{3}\pi {r^2}h\].
Giữ nguyên bán kính đáy của hình nón và giảm chiều cao của nó \(S\) lần thì thể tích của hình nón này là \(ABC\).\[{V_2} = \frac{1}{3}\pi {r^2}\frac{h}{2} = \frac{1}{2}.\frac{1}{3}\pi {r^2}h = \frac{1}{2}{V_1}\]
Thể tích của hình nón này giảm \(S.ABC\) lần so với ban đầu
Lời giải
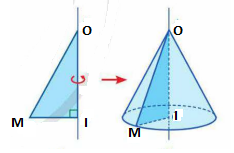
a) Xét tam giác \(OIM\) vuông tại \(I\),Theo pythagore ta có :
\(\begin{array}{l}O{M^2} = I{M^2} + O{I^2}\\O{M^2} = {3^2} + {4^2}\\O{M^2} = 25\\ \Rightarrow OM = 5\end{array}\).
Khi quay tam giác \(OIM\) quanh cạnh góc vuông \(OI\) thì đường gấp khúc \(OIM\) tạo thành hình nón có bán kính đáy \(r = IM = 3cm\), chiều cao \(h = OI = 4cm\)và đường sinh là cạnh huyền \(l = OM = 5cm\).
Vậy độ dài đường sinh của hình nón là \(5cm\).
b) Diện tích xung quanh hình nón là:\[{S_{xq}} = \pi rl = \pi .3.5 = 15\pi \left( {c{m^2}} \right)\]
c) Diện tích toàn phần hình nón là:
d) Thể tích hình nón là: \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.3^2}.4 = 12\pi \left( {c{m^3}} \right)\]
Lời giải
![Cho tam giác \[\Delta SO'A\] vuông tạ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/5-1769743781.png)
a) khi quay tam giác \[{60^ \circ }\] xung quanh trục \[30{\rm{ }}cm\], tao ra hình nón có:
bán kính đáy \(r = \frac{{BC}}{2} = 1dm\), đường sinh là \[{r_1},{h_1},{r_2},{h_2}\]
Diện tích xung quanh hình nón là:\[{60^ \circ }\]
b) Chiều cao của hình nón: \[h = \sqrt {{l^2} - {r^2}} = \sqrt {{{\left( {\sqrt 2 } \right)}^2} - 1} = 1dm\]
thể tích hình nón: \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .1.1 = \frac{1}{3}\pi \left( {d{m^3}} \right)\]
![Cho hình nón có bán kính đáy \[r\], đường cao \[h\] và đường sinh \[l\] như hình vẽ. Hãy thay dấu “\[?\]”bằng giá trị thích hợp và hoàn thành bảng sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/3-1769743706.png)