7 bài tập Xác định tâm và tính bán kính đường tròn ngoại tiếp, nội tiếp tam giác (có lời giải)
68 người thi tuần này 4.6 107 lượt thi 7 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Lời giải
a) Hình \[a)\], đường tròn \[\left( O \right)\]là đường tròn ngoại tiếp tam giác \[ABC\] vì nó đi qua ba đỉnh \[A,B,C\] của tam giác \[ABC\].
b) Hình \[d)\], đường tròn \[\left( O \right)\]là đường tròn nội tiếp tam giác \[ABC\] vì nó tiếp xúc ba cạnh \[AB,BC,CA\] của tam giác \[ABC\].
Lời giải
![Cho tam giác \[ABC\] vuông tại \[A\], có \[AB = 10cm\] và \[AC = \sqrt {21} cm\]. Tính bán kính đường tròn ngoại tiếp tam giác \[ABC\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/2-1769677434.png)
Xét \[ABC\] vuông tại \[A\], theo pythagore ta có:
\[\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\B{C^2} = {10^2} + {\left( {\sqrt {21} } \right)^2}\\B{C^2} = 121\\ \Rightarrow BC = \sqrt {121} = 11\left( {cm} \right)\end{array}\]
Tam giác \[ABC\] vuông tại \[A\] nên bán kính \[R\] đường tròn ngoại tiếp tam giác \[ABC\] bằng nữa cạnh huyền \[BC\] hay \[R = \frac{{BC}}{2} = \frac{{11}}{2} = 5,5\left( {cm} \right)\]
Lời giải
![Cho \[\Delta ABC\] vuông tại \[A\], có \[AB = 6cm\] và \[AC = 8cm\] ngoại tiếp đường tròn \[\left( {I;r} \right)\]. Tính \[r\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/3-1769677458.png)
Đường tròn \[\left( {I;r} \right)\] tiếp xúc với các cạnh \[AB,AC,BC\] theo thứ tự \[M,N,P\]
Ta có: \[{S_{AIB}} = \frac{1}{2}IM.AB = \frac{1}{2}r.AB\,\left( 1 \right);\,{S_{AIC}} = \frac{1}{2}IN.AC = \frac{1}{2}r.AC\,\left( 2 \right);\,{S_{BIC}} = \frac{1}{2}r.BC\,\left( 3 \right)\]
Cộng \[\left( 1 \right)\left( 2 \right)\left( 3 \right)\] vế theo vế, ta được: \[\frac{{{S_{AIB}} + {S_{AIC}} + {S_{BIC}}}}{{{S_{ABC}}}} = \frac{1}{2}r.\left( {AB + AC + BC} \right)\]
Mà \[{S_{ABC}} = \frac{1}{2}AB.AC = \frac{{6.8}}{2} = 24\left( {c{m^2}} \right)\] , \[BC = \sqrt {{6^2} + {8^2}} = \sqrt {100} = 10\left( {cm} \right)\]
Nên ta có: \[24 = \frac{1}{2}r\left( {6 + 8 + 10} \right) \Rightarrow r = 2\left( {cm} \right)\].
Lời giải
Gọi O là giao điểm của ba đường trung trực của tam giác đều ABC thì O đồng thời cũng là trọng tâm và trực tâm của tam giác. Ta có \({\rm{OA}} = {\rm{OB}} = {\rm{OC}} = \frac{2}{3}{\rm{AH}}\) (H là chân đường cao kẻ từ A) (Xem hình vẽ).
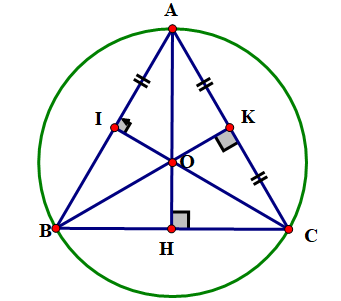
Do đó O là tâm của đường tròn ngoại tiếp tam giác đều ABC .
Mặt khác, xét tam giác AHB vuông tại H.
Theo định lí Pythagore, ta có:\({\rm{A}}{{\rm{B}}^2} = {\rm{A}}{{\rm{H}}^2} + {\rm{H}}{{\rm{B}}^2} \Rightarrow {\rm{A}}{{\rm{H}}^2} = {\rm{A}}{{\rm{B}}^2} - {\rm{H}}{{\rm{B}}^2} = {{\rm{a}}^2} - {\left( {\frac{{\rm{a}}}{2}} \right)^2}\)\( \Rightarrow {\rm{AH}} = \sqrt {{{\rm{a}}^2} - {{\left( {\frac{{\rm{a}}}{2}} \right)}^2}} = \frac{{{\rm{a}}\sqrt 9 }}{2}\)
\( \Rightarrow {\rm{AO}} = \frac{2}{3}{\rm{AH}} = \frac{2}{3} \cdot \frac{{{\rm{a}}\sqrt 3 }}{2} = \frac{{{\rm{a}}\sqrt 3 }}{3}\)(Tính chất trọng tâm)
Vậy đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm tam giác và có bán kính \(\frac{{{\rm{a}}\sqrt 3 }}{3}\).
Lời giải
a) (Xem hình vẽ).
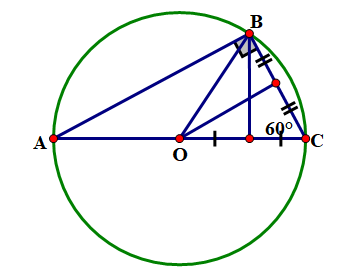
Tam giác ANC vuông tại B có nên tam giác ABC là nửa tam giác đều
Theo bài toán 1 ta có bán kính đường tròn ngoại tiếp là \(\frac{{{\rm{AC}}}}{2} = \frac{6}{2} = 3(\;{\rm{cm}})\)và tâm O là trung điểm cạnh huyền AC .
b) Dễ thấy tam giác BCD đều (Theo bài toán 2).
Gọi I là trọng tâm của tam giác BCD, ta có I là tâm của đường tròn ngoại tiếp vì cạnh của tam giác đều BCD là \(3(\;{\rm{cm}})\) nên bán kính của đường tròn ngoại tiếp tam giác đều BCD là \(\frac{{3\sqrt 3 }}{3}\) (Xem lời giải bài toán 2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hình vẽ sau : a) Hình nào có đường tròn \[\left( O \right)\]ngoại tiếp tam giác \[ABC\]? Giải thích ? b) Hình nào có đường tròn \[\left( O \right)\]nội tiếp tam giác\[ABC\]? Giải thích ? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/1-1769677406.png)