Chuyên đề Toán 11 KNTT Bài 7. Phép đồng dạng có đáp án
32 người thi tuần này 4.6 636 lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 7 (có lời giải) - Đề 1
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 3
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 2
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 1
Đề kiểm tra Bài tập cuối chương 6 (có lời giải) - Đề 3
Danh sách câu hỏi:
Lời giải
Lời giải:
Đối tượng toán học liên quan đến phép đồng dạng cho phép ta thể hiện các hình chỉ giống nhau về hình dạng còn kích thước có thể khác nhau. Chúng ta sẽ cùng tìm hiểu trong bài học này.
Lời giải
Lời giải:
a) Qua đo đạc, ta thấy chiều dài và chiều rộng của tấm ảnh lớn tương ứng gấp 2 lần chiều dài và chiều rộng của tấm ảnh nhỏ.
b) Lấy các điểm A, B và A', B' tương ứng như hình vẽ.

Qua đo đạc ta thấy A'B' = 2AB.
Lời giải
Lời giải:
+ Phép dời hình cũng là phép đồng dạng với tỉ số k = 1.
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép dời hình. Khi đó M'N' = MN (phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số 1.
+ Phép vị tự với tỉ số k là phép đồng dạng với tỉ số đồng dạng |k|.
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép vị tự tỉ số k. Khi đó \(\overrightarrow {M'N'} = k\overrightarrow {MN} \)\( \Rightarrow M'N' = \left| k \right|MN\). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số |k| (|k| > 0).
Lời giải
Lời giải:
Lấy hai điểm M, N bất kì. Gọi M', N' tương ứng là ảnh của M, N qua phép đồng dạng f với tỉ số k1 thì ta có M'N' = k1MN.
Gọi M", N" tương ứng là ảnh của M', N' qua phép đồng dạng g với tỉ số k2 thì ta có M"N" = k2M'N'.
Khi đó ta có M"N" = k2 M'N' = k2 . (k1MN) = (k1.k2)MN.
Do đó, M", N" tương ứng là ảnh của M, N qua phép đồng dạng với tỉ số k1.k2.
Từ đó suy ra điều phải chứng minh.
Lời giải
Lời giải:
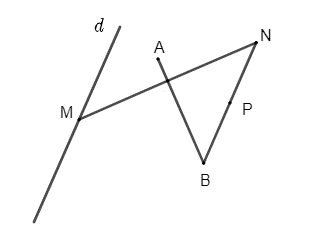
Vì N là điểm đối xứng của M qua đường thẳng AB nên ta có phép đối xứng trục AB biến điểm M thành điểm N.
Ta có P là trung điểm của BN nên \(\overrightarrow {BP} = \frac{1}{2}\overrightarrow {BN} \), do đó ta có phép vị tự tâm B, tỉ số \(\frac{1}{2}\) biến điểm N thành điểm P.
Như vậy, phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\,\frac{1}{2}} \right)}}\) biến điểm M thành điểm P.
Mặt khác M thuộc đường thẳng d cố định, A và B cố định, do đó P thuộc đường thẳng d' cố định là ảnh của đường thẳng d qua phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\,\frac{1}{2}} \right)}}\).
Vậy P thuộc một đường thẳng cố định.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.


