Giải SGK Toán 11 KNTT Bài 27. Thể tích có đáp án

Thể tích của căn phòng là: V = 4 × 5 × 3 = 60 (m³).

Vì mỗi mét khối của phòng cần công suất điều hòa 200 BTU nên căn phòng cần điều hòa có công suất là: 60 × 200 = 12 000 (BTU).

Vậy bác An cần mua loại điều hòa có công suất là 12 000 BTU.

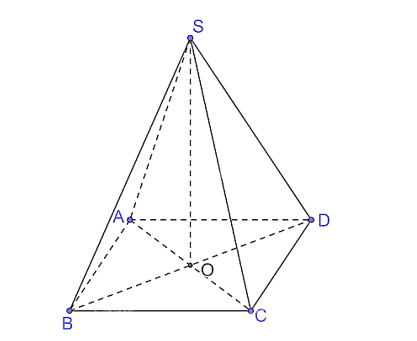
Gọi O là giao điểm của AC và BD. Vì S.ABCD là hình chóp đều nên SO ^ (ABCD).

Xét tam giác BCD vuông tại C, có $BD=\sqrt{B{C}^2+C{D}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$  .

Vì ABCD là hình vuông nên O là trung điểm của BD, suy ra $BO=\frac{BD}{2}=\frac{a\sqrt{2}}{2}$  .

Xét tam giác SOB vuông tại O, có $SO=\sqrt{S{B}^2-O{B}^2}=\sqrt{b^2-\frac{a^2}{2}}$ .

Ta có . $V_{S.ABCD}=\frac{1}{3}\cdot S_{ABCD}\cdot SO=\frac{1}{3}\cdot a^2\cdot \sqrt{b^2-\frac{a^2}{2}}=\frac{1}{3}\cdot a^2\cdot \sqrt{\frac{2b^2-a^2}{2}}$ .

a) Ta có $S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{a^2\sqrt{3}}{4}$  ; $S_{ABC}=\frac{{\left(2a\right)}^2\sqrt{3}}{4}=a^2\sqrt{3}$  .

Khi đó    $V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{1}{3}\cdot \left(S_{ABC}+S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}+\sqrt{S_{ABC}\cdot S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}}\right)\cdot H{H}^{\text{'}}$        

$=\frac{1}{3}\cdot \left(a^2\sqrt{3}+\frac{a^2\sqrt{3}}{4}+\sqrt{a^2\sqrt{3}\cdot \frac{a^2\sqrt{3}}{4}}\right)\cdot h$.

$=\frac{1}{3}\cdot \left(a^2\sqrt{3}+\frac{a^2\sqrt{3}}{4}+\frac{a^2\sqrt{3}}{2}\right)\cdot h$

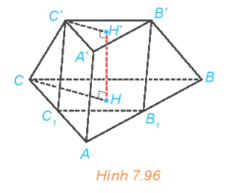
b) Vì ABC.A'B'C' là khối chóp cụt đều nên (ABC) // (A'B'C') mà (AB₁C₁) Ì (ABC) nên (AB₁C₁) // (A'B'C').

Xét tam giác ABC có B₁, C₁ lần lượt là trung điểm của AB, AC nên B₁C₁ là đường trung bình của tam giác ABC do đó B₁C₁ // BC và $B_1{C}_1=\frac{BC}{2}=\frac{2a}{2}=a$  .

Lại có B'C' // BC nên B₁C₁ // B'C' và B'C' = B₁C₁ = a nên B₁C₁C'B' là hình bình hành.

Vì B₁, C₁ lần lượt là trung điểm của AB, AC nên AB₁ = AC₁ = a.

Vì A'B' // AB₁ và A'B' = AB₁ = a nên A'B'B₁A là hình bình hành.

Vì A'C' // AC₁ và A'C' = AC₁ = a nên A'C'C₁A là hình bình hành.

Do đó AB₁C₁.A'B'C' là hình lăng trụ.

Vì hình lăng trụ AB₁C₁.A'B'C' có cùng chiều cao với khối chóp cụt đều ABC.A'B'C' nên $V_{A{B}_1{C}_1.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}.H{H}^{\text{'}}=\frac{a^2\sqrt{3}}{4}\cdot h$  .

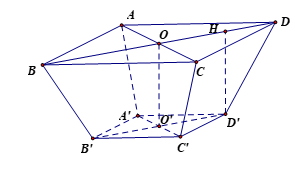
Sọt đựng đồ có dạng hình chóp cụt đều ABCD.A'B'C'D'.

Ta có S₁ = S_ABCD = 60² = 3 600(cm²), S₂ = S_A'B'C'D' = 30² = 900 (cm²).

Kẻ D'H ^ BD tại H.

Gọi O và O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'.

Vì OO' ^ (ABCD) nên OO' ^ OH, OO' ^ (A'B'C'D') nên OO' ^ B'D'.

Do đó OHD'O' là hình chữ nhật, suy ra O'D' = OH, OO' = HD'.

Xét tam giác B'C'D' vuông tại C', có

$B^{\text{'}}{D}^{\text{'}}=\sqrt{B^{\text{'}}{C^{\text{'}}}^2+C^{\text{'}}{D^{\text{'}}}^2}=\sqrt{{30}^2+{30}^2}=30\sqrt{2}$ (cm).

Vì O' là trung điểm của B'D' nên $D^{\text{'}}{O}^{\text{'}}=\frac{D^{\text{'}}{B}^{\text{'}}}{2}=15\sqrt{2}$  (cm).

Xét tam giác BCD vuông tại C, có

$BD=\sqrt{B{C}^2+C{D}^2}=\sqrt{{60}^2+{60}^2}=60\sqrt{2}$ (cm).

Mà O là trung điểm của BD nên $DO=\frac{DB}{2}=30\sqrt{2}$  (cm).

Có HD = DO – OH =  (cm).

Xét tam giác DHD' vuông tại H, có

$D^{\text{'}}H=\sqrt{{}^2-H{D}^2}=\sqrt{{50}^2-{\left(15\sqrt{2}\right)}^2}=5\sqrt{82}$ (cm).

Do đó $5\sqrt{82}$   (cm).

$V_{ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}D}=\frac{1}{3}\left(S_1+S_2+\sqrt{S_1\cdot S_2}\right)\cdot$

$=\frac{1}{3}\left(3600+900+\sqrt{3600\cdot 900}\right)\cdot 5\sqrt{82}=10500\sqrt{82}$(cm³).

Gọi G là hình chiếu của S trên mặt phẳng (ABC). Vì S.ABC là khối chóp đều nên G là trọng tâm của tam giác ABC. Có SG ^ (ABC).

Giả sử AG Ç BC tại D, khi đó D là trung điểm của BC, AD ^ BC.

Xét tam giác ABC đều cạnh a, AD là đường cao nên $AD=\frac{a\sqrt{3}}{2}$ , $S_{ABC}=\frac{a^2\sqrt{3}}{4}$ .

Vì $AG=\frac{2}{3}AD=\frac{a\sqrt{3}}{3}$ .

Xét tam giác SGA vuông tại G, có$SG=\sqrt{S{A}^2-A{G}^2}=\sqrt{b^2-\frac{a^2}{3}}=\sqrt{\frac{3b^2-a^2}{3}}$ .

Ta có $V_{S.ABC}=\frac{1}{3}\cdot S_{ABC}\cdot SG=\frac{1}{3}\cdot \frac{a^2\sqrt{3}}{4}\cdot \sqrt{\frac{3b^2-a^2}{3}}=\frac{a^2\sqrt{3b^2-a^2}}{12}$  .

Khi đó thể tích khối tứ diện đều có cạnh bằng a là: $\frac{a^2\sqrt{3a^2-a^2}}{12}=\frac{a^3\sqrt{2}}{12}$.