Câu hỏi:
25/05/2022 252Trong khoảng \[\left( {0\,\,;\,\,\frac{\pi }{2}} \right)\]phương trình \[si{n^2}4x + 3sin4xcos4x - 4co{s^2}4x = 0\;\] có:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trường hợp 1:\[\cos 4x = 0 \Leftrightarrow 4x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\]
Khi đó\[{\sin ^2}4x = 1\]
Thay vào phương trình ta có:\[1 + 3.0 - 4.0 = 0 \Leftrightarrow 1 = 0\,\,\left( {V\^o \,\,l\'y } \right)\]
\[ \Rightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\] không là nghiệm của phương trình.
Trường hợp 2:\[\cos 4x \ne 0 \Leftrightarrow x \ne \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\]
Chia cả 2 vế của phương trình cho \[{\cos ^2}4x\] ta được:
\[\frac{{{{\sin }^2}4x}}{{{{\cos }^2}4x}} + 3\frac{{\sin 4x}}{{\cos 4x}} - 4 = 0 \Leftrightarrow {\tan ^2}4x + 3\tan 4x - 4 = 0\]
Đặt tan4x=t. Khi đó phương trình trở thành
\[{t^2} + 3t - 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1}\\{t = - 4}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{tan4x = 1}\\{tan4x = - 4}\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = \frac{\pi }{4} + k\pi }\\{4x = arctan( - 4) + k\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{1}{4}arctan( - 4) + \frac{{k\pi }}{4}}\end{array}} \right.(k \in Z)\)
Xét nghiệm\[x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right),\,x \in \left( {0;\frac{\pi }{2}} \right)\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < \frac{\pi }{{16}} + \frac{{k\pi }}{4} < \frac{\pi }{2}}\\{k \in Z}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < \frac{1}{{16}} + \frac{k}{4} < \frac{1}{2}}\\{k \in Z}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - \frac{1}{4} < k < \frac{7}{4}}\\{k \in Z}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{k = 0}\\{k = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}}}\\{x = \frac{{5\pi }}{{16}}}\end{array}} \right.\)
Xét nghiệm\[x = \frac{1}{4}\arctan \left( { - 4} \right) + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right);\,\,x \in \left( {0;\frac{\pi }{2}} \right)\]
\(\left\{ {\begin{array}{*{20}{c}}{0 < \frac{1}{4}arctan( - 4) + \frac{{k\pi }}{4} < \frac{\pi }{2}}\\{k \in Z}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - \frac{1}{4}arctan( - 4) < \frac{{k\pi }}{4} < \frac{\pi }{2} - \frac{1}{4}arctan( - 4)}\\{k \in Z}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0,42 < k < 2,42}\\{k \in Z}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{k = 1}\\{k = 2}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{1}{4}arctan( - 4) + \frac{\pi }{4}}\\{x = \frac{1}{4}arctan( - 4) + \frac{\pi }{2}}\end{array}} \right.\)
Vậy phương trình có 4 nghiệm thuộc khoảng\[\left( {0\,\,;\,\,\frac{\pi }{2}} \right)\]
Đáp án cần chọn là: D
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\[4{\sin ^2}x - 4\sin x - 3 = 0\]
Đặt\[\sin x = t\,\,\left( { - 1 \le t \le 1} \right)\]khi đó phương trình có dạng:
\[4{t^2} - 4t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \frac{3}{2}(ktm)}\\{t = - \frac{1}{2}(tm)}\end{array}} \right.\]
\[t = - \frac{1}{2} \Leftrightarrow sinx = - \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{6} + k2\pi }\\{x = - \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.(k \in Z)\]
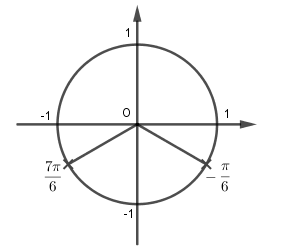
Vây số vị trí biểu diễn các nghiệm của phương trình\[4{\sin ^2}x - 4\sin x - 3 = 0\]trên đường tròn lượng giác là 2 điểm như hình trên.
Đáp án cần chọn là: C
Lời giải
Bước 1:
\[\sin x + \sqrt 3 \cos x = \sqrt 2 \Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 2 }}{2}\]
\[\Leftrightarrow \sin x\cos \frac{\pi }{3} + \cos x\sin \frac{\pi }{3} = \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin \left( {x + \frac{\pi }{3}} \right) = \sin \frac{\pi }{4}\]
Bước 2:
\(\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + \frac{\pi }{3} = \frac{\pi }{4} + k2\pi }\\{x + \frac{\pi }{3} = \frac{\pi }{4} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{{12}} + k2\pi }\\{x = \frac{{5\pi }}{{12}} + k2\pi }\end{array}} \right.(k \in \mathbb{Z})\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\alpha = - \frac{\pi }{{12}}}\\{\beta = \frac{{5\pi }}{{12}}}\end{array}} \right.\)
(Vì\[ - \frac{\pi }{{12}}\] và\[\frac{{5\pi }}{{12}}\] đều thỏa mãn điều kiện đề bài)
\[ \Rightarrow \alpha .\beta \; = \frac{{ - 5{\pi ^2}}}{{144}}\]
Đáp án cần chọn là: B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Nhắn tin Zalo