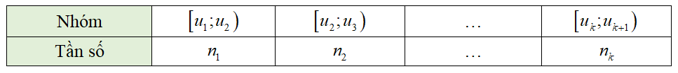Bộ 10 đề thi cuối kì 1 Toán 11 Chân trời sáng tạo có đáp án - Đề 6
24 người thi tuần này 4.6 2 K lượt thi 38 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Danh sách câu hỏi:
Câu 1
\[\frac{{1 + \sqrt 3 }}{2}\].
\[\frac{{1 - \sqrt 3 }}{2}\].
\[\frac{{\sqrt 3 }}{2}\].
\[\frac{1}{2}\].
Lời giải
Đáp án đúng là: A
Có \[\cos \alpha + \sin \alpha \]\[ = \cos \frac{\pi }{6} + \sin \frac{\pi }{6}\]\[ = \frac{{\sqrt 3 }}{2} + \frac{1}{2} = \frac{{1 + \sqrt 3 }}{2}\].
Câu 2
\[\cos 2a = {\cos ^2}a - {\sin ^2}a\].
\[\cos 2a = {\cos ^2}a + {\sin ^2}a\].
\[\cos 2a = 2{\cos ^2}a + 1\].
\[\cos 2a = 2\sin a\cos a\].
Lời giải
Đáp án đúng là: A
Ta có \[\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\].
Câu 3
\(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k2\pi |k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {0;\pi } \right\}\).
Lời giải
Đáp án đúng là: C
Hàm số \(y = \frac{1}{{\sin x}}\) xác định khi và chỉ khi \(\sin x \ne 0 \Leftrightarrow x \ne k\pi ,k \in \mathbb{Z}\).
Câu 4
\(x = 20^\circ + k.45^\circ ,{\rm{ }}k \in \mathbb{Z}.\)
\(x = 30^\circ + k.45^\circ ,{\rm{ }}k \in \mathbb{Z}.\)
\(x = 20^\circ + k.90^\circ ,{\rm{ }}k \in \mathbb{Z}.\)
\(x = 35^\circ + k.90^\circ ,{\rm{ }}k \in \mathbb{Z}.\)
Lời giải
Đáp án đúng là: A
Điều kiện \(\sin \left( {4x - 20^\circ } \right) \ne 0\)\( \Leftrightarrow 4x - 20^\circ \ne k.180^\circ \)\( \Leftrightarrow x \ne 5^\circ + k.45^\circ ,k \in \mathbb{Z}\).
\(\cot \left( {4x - 20^\circ } \right) = \frac{1}{{\sqrt 3 }}\)\( \Leftrightarrow 4x - 20^\circ = 60^\circ + k.180^\circ \)\( \Leftrightarrow x = 20^\circ + k.45^\circ ,k \in \mathbb{Z}\).
Kết hợp điều kiện, ta có nghiệm của phương trình là \(x = 20^\circ + k.45^\circ ,k \in \mathbb{Z}\).
Câu 5
1; 1; 1; 1; 1; ....
\(1; - \frac{1}{2};\frac{1}{4}; - \frac{1}{8};\frac{1}{{16}};...\).
1; 3; 5; 7; 9; ….
\(1;\frac{1}{2};\frac{1}{4};\frac{1}{8};\frac{1}{{16}};...\).
Lời giải
Đáp án đúng là: C
Xét đáp án A: 1; 1; 1; 1; 1; 1; …đây là dãy không đổi nên không tăng không giảm. Loại A.
Xét đáp án B: \(1; - \frac{1}{2};\frac{1}{4}; - \frac{1}{8};\frac{1}{{16}};...\) có \({u_1} > {u_2} < {u_3}\) nên loại B.
Xét đáp án C: 1; 3; 5; 7; 9; … có \({u_n} < {u_{n + 1}},n \in {\mathbb{N}^*}\) nên đây là dãy tăng. Chọn C.
Xét đáp án D: \(1;\frac{1}{2};\frac{1}{4};\frac{1}{8};\frac{1}{{16}};...\) có \({u_1} > {u_2} > {u_3} > ... > {u_n} > ...\). Loại D.
Câu 6
\(\frac{1}{2};\frac{3}{2};\frac{5}{2};\frac{7}{2};\frac{9}{2}\).
\(1;1;1;1;1\).
\( - 8; - 6; - 4; - 2;0\).
\(3;1; - 1; - 2; - 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\(d = 7\).
\(d = 5\).
\(d = 8\).
\(d = 6\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
\(2\).
\( - 2\).
\( - 9\).
\(9\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Dãy số \(\left( {{u_n}} \right)\) có giới hạn là số a (hay \({u_n}\) dần tới a) khi \(n \to + \infty \), nếu \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\).
Dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0 khi \(n\) dần tới vô cực, nếu \(\left| {{u_n}} \right|\) có thể lớn hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.
Dãy số \(\left( {{u_n}} \right)\) có giới hạn là \( + \infty \) nếu \({u_n}\) có thể nhỏ hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Dãy số \(\left( {{u_n}} \right)\) có giới hạn là \( - \infty \)khi \(n \to + \infty \) nếu \({u_n}\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
\[\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) - g\left( x \right)} \right] = L - M\].
\[\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) \cdot g\left( x \right)} \right] = L \cdot M\].
\[\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{L}{M}\].
\[\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
\[2\].
\[1\].
\[ + \infty \].
\[0\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty \).
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = - \infty \).
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{{x^5}}} = + \infty \).
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt x }} = + \infty \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
\(L = 1\).
\(L = \frac{1}{2}\).
\(L = - \frac{1}{2}\).
\(L = - \frac{3}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
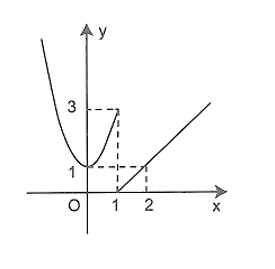
Câu 16
\(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = f\left( {{x_0}} \right)\).
\(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\).
\(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = f\left( {{x_0}} \right)\).
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
\(\left( { - 3;2} \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
\(\left( { - 4;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
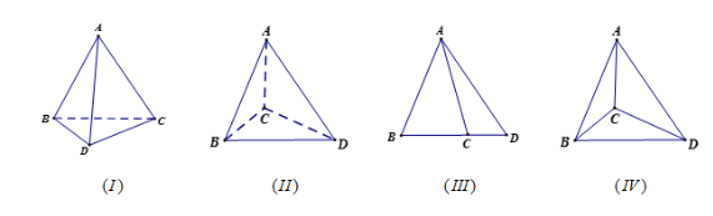
Câu 19
(I), (II).
(I), (II), (III), (IV).
(I), (III).
(I), (II), (III).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Hai đường thẳng phân biệt không song song thì chéo nhau.
Hai đường thẳng không có điểm chung thì chéo nhau.
Hai đường thẳng chéo nhau thì không có điểm chung.
Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
song song.
chéo nhau.
cắt nhau.
trùng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
\(AB\).
\(CD\).
\(BC\).
\(AD\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Nếu \(d{\rm{//}}\left( \alpha \right)\) thì trong \(\left( \alpha \right)\) tồn tại đường thẳng \(a\) sao cho \(a{\rm{//}}d\).
Nếu \(d{\rm{//}}\left( \alpha \right)\) và đường thẳng \(b \subset \left( \alpha \right)\) thì \(b{\rm{//}}d\).
Nếu \(d{\rm{//}}c \subset \left( \alpha \right)\) thì \(d{\rm{//}}\left( \alpha \right)\).
Nếu \(d \cap \left( \alpha \right) = A\) và đường thẳng \(d' \subset \left( \alpha \right)\) thì \(d\) và \(d'\) hoặc cắt nhau hoặc chéo nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
\(MN{\rm{//}}\left( {ABCD} \right)\).
\(MN{\rm{//}}\left( {SAB} \right)\).
\(MN{\rm{//}}\left( {SCD} \right)\).
\(MN{\rm{//}}\left( {SBC} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
\(MG{\rm{//}}\left( {BCD} \right)\).
\(MG{\rm{//}}\left( {ACD} \right)\).
\(MG{\rm{//}}\left( {ABD} \right)\).
\(MG{\rm{//}}\left( {ABC} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Nếu \(\left( \alpha \right){\rm{//}}\left( \beta \right)\) và \(a \subset \left( \alpha \right),b \subset \left( \beta \right)\) thì \(a{\rm{//}}b\).
Nếu \(a{\rm{//}}\left( \alpha \right)\) và \(b{\rm{//}}\left( \beta \right)\) thì \(a{\rm{//}}b\).
Nếu \(\left( \alpha \right){\rm{//}}\left( \beta \right)\) và \(a \subset \left( \alpha \right)\) thì \(a{\rm{//}}\left( \beta \right)\).
Nếu \(a{\rm{//}}b\) và \(a \subset \left( \alpha \right),b \subset \left( \beta \right)\) thì \(\left( \alpha \right){\rm{//}}\left( \beta \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
\(\left( {BCA'} \right)\).
\(\left( {BC'D} \right)\).
\(\left( {A'C'C} \right)\).
\(\left( {BDA'} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
\(D\).
Trung điểm của \(CD\).
Trung điểm của \(BD\).
Trọng tâm tam giác \(BCD\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
Bảng tần số ghép nhóm.
Bảng tần số nhóm.
Bảng tần số, tần suất ghép nhóm.
Bảng ghép nhóm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
\(35\).
\(40\).
\(25\).
\(30\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
\[19,4\].
\[18,4\].
\[20,4\].
\[21,4\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.