20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 4. Hàm số lượng giác và đồ thị (Đúng sai - Trả lời ngắn) có đáp án
59 người thi tuần này 4.6 340 lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Danh sách câu hỏi:
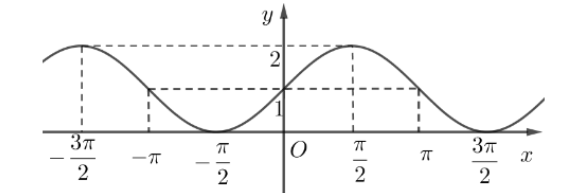
Câu 1
Lời giải
B
Điều kiện xác định: \(\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \).
Vậy tập xác định: \(D = \mathbb{R}{\rm{\backslash }}\left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Câu 2
Lời giải
C
Hàm số \(y = 2\sin x\)có tập xác định là \(\mathbb{R}\).
Câu 3
Lời giải
C
Điều kiện:\(\sin x \ne 0 \Leftrightarrow x \ne k\pi ,k \in \mathbb{Z}\), suy ra tập xác định của hàm số \(y = \cot x\) là \(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
Câu 4
Lời giải
B
Điều kiện xác định của hàm số: \(\cos 2x \ne 0 \Leftrightarrow 2x \ne \frac{\pi }{2} + k\pi \Leftrightarrow x \ne \frac{\pi }{4} + k\frac{\pi }{2},{\rm{ }}k \in \mathbb{Z}\).
Vậy tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\frac{\pi }{2},k \in \mathbb{Z}} \right\}\).
Lời giải
C
Hàm số \(y = \tan x\), \(y = \cot x\) là hàm số tuần hoàn với chu kỳ \(T = \pi \).
Hàm số \(y = \sin 2x\) là hàm số tuần hoàn với chu kỳ \(T = \frac{{2\pi }}{2} = \pi \).
Hàm số \(y = \cos x\) là hàm số tuần hoàn với chu kỳ \(T = 2\pi \).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(y = \tan x\) nghịch biến trong \(\left( {0;\;\frac{\pi }{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \(h\left( t \right) = 31 + 3\sin \frac{\pi }{{12}}\left( {t - 9} \right)\), với h tính bằng độ C và t là thời gian trong ngày tính bằng giờ (0 < t ≤ 24). Tính nhiệt độ ngoài trời của thành phố đó vào lúc 19 giờ.
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \(h\left( t \right) = 31 + 3\sin \frac{\pi }{{12}}\left( {t - 9} \right)\), với h tính bằng độ C và t là thời gian trong ngày tính bằng giờ (0 < t ≤ 24). Tính nhiệt độ ngoài trời của thành phố đó vào lúc 19 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.