21 câu Trắc nghiệm Toán 10 Cánh diều Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng (Đúng-sai, trả lời ngắn) có đáp án
37 người thi tuần này 4.6 224 lượt thi 21 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Câu 1
A. Trên khoảng \[\left( { - \infty ;1} \right)\], hàm số đồng biến.
B. Hàm số nghịch biến trên khoảng \[\left( {2; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;2} \right)\].
C. Trên khoảng \[\left( {3; + \infty } \right)\], hàm số nghịch biến.
D. Hàm số nghịch biến trên khoảng \[\left( {4; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;4} \right)\].
Lời giải
Đáp án đúng là: D
Đỉnh của parabol có hoành độ: \[{x_I} = - \frac{b}{{2a}} = 2\].
Vì \(a = - 1 < 0\) nên hàm số đồng biến trên khoảng \[\left( { - \infty ;2} \right)\] và nghịch biến trên khoảng \[\left( {2; + \infty } \right)\].
Mà \[\left( { - \infty ;1} \right) \subset \left( { - \infty ;2} \right)\] và \[\left( {3; + \infty } \right) \subset \left( {2; + \infty } \right)\].
Vậy khẳng định D sai.
Câu 2
A. \(\left( {1; + \infty } \right)\).
B. \(\left( { - 2; + \infty } \right)\).
C. \(\left( { - \infty ;1} \right)\).
D. \(\left( { - 3; + \infty } \right)\).
Lời giải
Đáp án đúng là: A
Ta có hàm số \(\left( P \right):\,y = f\left( x \right) = {x^2} - 2x + 3\) là hàm số bậc hai có hệ số \(a = 1\) nên \[\left( P \right)\] có bề lõm hướng lên.
Hoành độ đỉnh của parabol \({x_I} = \frac{{ - b}}{{2a}} = 1\). Do đó hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
Câu 3
A. \(I\left( {0;1} \right)\).
B. \(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\).
C. \(I\left( { - \frac{1}{3};\,\frac{2}{3}} \right)\).
D. \(I\left( {\frac{1}{3};\, - \frac{2}{3}} \right)\).
Lời giải
Đáp án đúng là: B
Hoành độ đỉnh của \(\left( P \right):y = 3{x^2} - 2x + 1\) là \(x = - \frac{b}{{2a}} = \frac{1}{3}\)\( \Rightarrow y = 3 \cdot {\left( {\frac{1}{3}} \right)^2} - 2 \cdot \frac{1}{3} + 1 = \frac{2}{3}\).
Vậy \(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\).
Câu 4
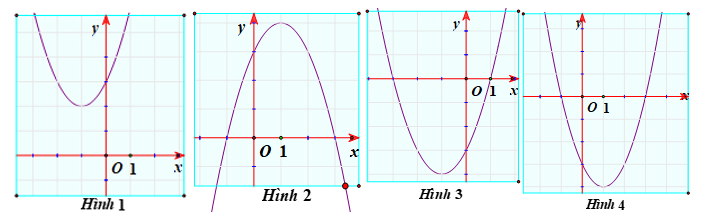
A. Hình \[1\].
B. Hình \[2\].
C. Hình \[3\].
D. Hình \[4\].
Lời giải
Đáp án đúng là: D
Dựa vào đồ thị có:
\[\left( P \right):y = f\left( x \right) = {x^2} - 2x - 3\] có \[a = 1 > 0\] nên \[\left( P \right)\] có bề lõm hướng lên (loại hình \[2\]).
\[\left( P \right)\] có đỉnh \[I\] có \[{x_I} = 1\] (loại hình \[1\] và \[3\]).
Vậy \[\left( P \right):y = f\left( x \right) = {x^2} - 2x - 3\] có đồ thị là hình \[4\].
Câu 5
A. \(\left\{ \begin{array}{l}a = 3\\b = - 2\end{array} \right..\)
B. \(\left\{ \begin{array}{l}a = 3\\b = 2\end{array} \right..\)
C. \(\left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right..\)
D. \(\left\{ \begin{array}{l}a = 2\\b = - 3\end{array} \right..\)
Lời giải
Đáp án đúng là: C
Ta có: \({x_I} = - 1 \Rightarrow - \frac{4}{{2a}} = - 1 \Rightarrow a = 2.\)
Hơn nữa \(I \in \left( P \right)\) nên \( - 5 = a - 4 - b \Rightarrow b = 3.\)
Câu 6
A. \[a > 0\], \[b > 0\], \[c > 0\].
B. \[a > 0\], \[b < 0\], \[c < 0\].
C. \[a < 0\], \[b < 0\], \[c > 0\].
D. \[a < 0\], \[b > 0\], \[c > 0\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\).
B. \(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\).
C. \(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\).
D. \(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{{12}}\).
B. Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{{12}}\).
C. Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{3}\).
D. Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(m = 1.\)
B. \(m = 2.\)
C. \(m = - 2.\)
D. \(m = - 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(T = 3\).
B. \(T = \frac{1}{2}\).
C. \(T = \frac{9}{2}\).
D. \(T = - \frac{3}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(y = {x^2} - x + 1\).
B. \(y = {x^2} - x - 1\).
C. \(y = {x^2} + x - 1\).
D. \(y = {x^2} + x + 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.