Chuyên đề Toán 11 CTST Bài tập cuối chuyên đề 2 có đáp án

Đáp án đúng là: D

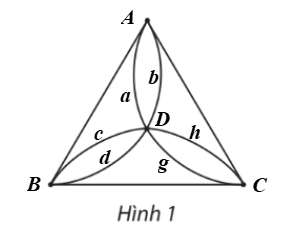
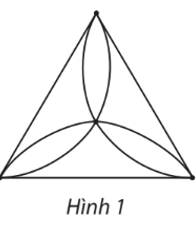
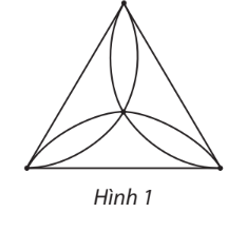
Gọi các đỉnh của đồ thị ở Hình 1 là: A, B, C, D (hình vẽ). Do đó đồ thị có 4 đỉnh.

Các cạnh của đồ thị ở Hình 1 là: AB, BC, CA, a, b, c, d, g, h. Do đó đồ thị có 9 cạnh.

Vậy ta chọn phương án D.

Đáp án đúng là: B

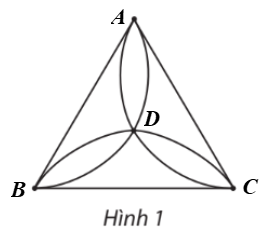
Gọi các đỉnh của đồ thị ở Hình 1 là: A, B, C, D (hình vẽ).

Ta có d(A) = d(B) = d(C) = 4 và d(D) = 6.

Tổng tất cả bậc của các đỉnh của đồ thị ở Hình 1 là: 4 + 4 + 4 + 6 = 18.

Vậy ta chọn phương án B.

Đáp án đúng là: C

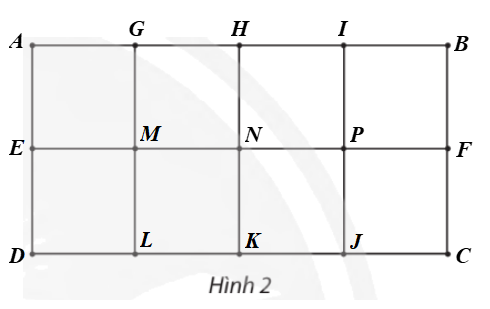
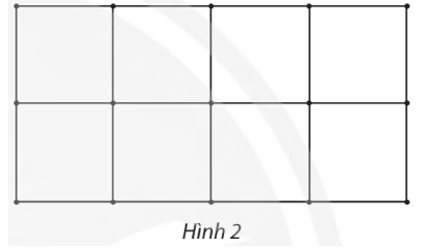
Gọi tên các đỉnh của đồ thị ở Hình 2 như hình vẽ.

Ta có:

⦁ d(A) = d(B) = d(C) = d(D) = 2;

⦁ d(E) = d(F) = d(G) = d(H) = d(I) = d(J) = d(K) = d(L) = 3;

⦁ d(M) = d(N) = d(P) = 4.

Suy ra các đỉnh E, F, G, H, I, J, K, L có bậc lẻ.

Vậy đồ thị ở Hình 2 có 8 đỉnh bậc lẻ.

Do đó ta chọn phương án C.

Đáp án đúng là: C

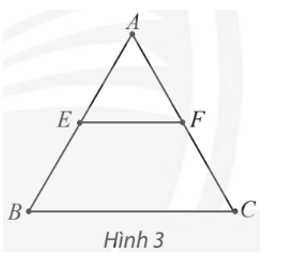
Ta có d(A) = d(B) = d(C) = 2 và d(E) = d(F) = 3.

Suy ra đồ thị ở Hình 2 có đúng hai đỉnh bậc lẻ là đỉnh E và đỉnh F.

Do đó đồ thị ở Hình 2 có đường đi Euler xuất phát từ đỉnh E đến đỉnh F (hoặc từ đỉnh F đến đỉnh E) nhưng không có chu trình Euler.

Vậy ta chọn phương án C.

Đáp án đúng là: B

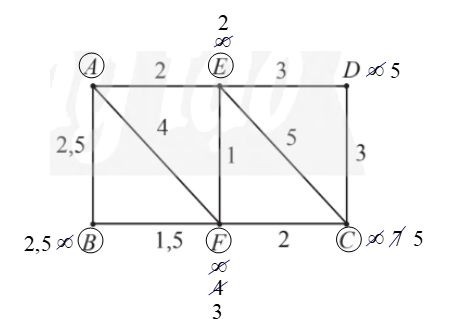
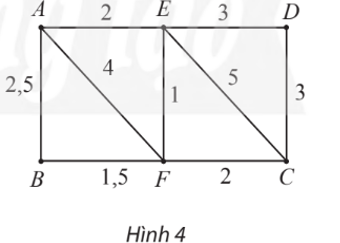
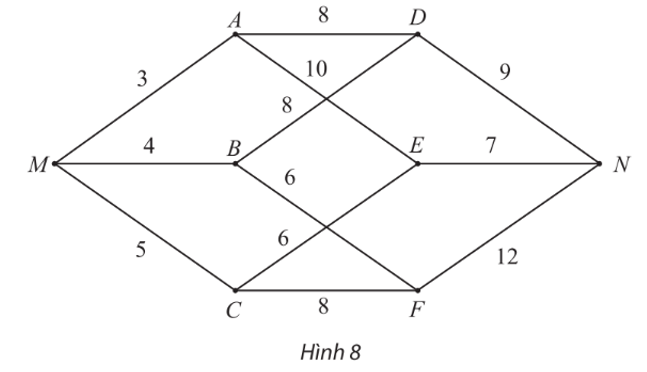
– Gán nhãn cho A bằng 0 (tức là, n_A = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.

– Tại các đỉnh kề với A, gồm E, F, B, ta có:

⦁ n_E = n_A + w_AE = 0 + 2 = 2. Vì 2 < ∞ nên ta đổi nhãn của E thành 2.

⦁ n_F = n_A + w_AF = 0 + 4 = 4. Vì 4 < ∞ nên ta đổi nhãn của F thành 4.

⦁ n_B = n_A + w_AB = 0 + 2,5 = 2,5. Vì 2,5 < ∞ nên ta đổi nhãn của B thành 2,5.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần A nhất, chỉ tính các đỉnh khác A).

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E gồm D, C, F, ta có:

⦁ n_D = n_E + w_ED = 2 + 3 = 5. Vì 5 < ∞ nên ta đổi nhãn của D thành 5.

⦁ n_C = n_E + w_EC = 2 + 5 = 7. Vì 7 < ∞ nên ta đổi nhãn của C thành 7.

⦁ n_F = n_E + w_EF = 2 + 1 = 3. Vì 3 < 4 (4 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 3.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần A thứ hai).

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B chỉ có F, ta có:

n_F = n_B + w_BF = 2,5 + 1,5 = 4. Vì 4 > 3 (3 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 3.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ ba).

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F chỉ có C, ta có:

n_C = n_F + w_FC = 3 + 2 = 5. Vì 5 < 7 (7 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 5.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C, D (đều có nhãn là 5), nhưng do ta cần tìm đường đi ngắn nhất từ A đến C nên ta ưu tiên khoanh tròn đỉnh C (đỉnh gần A thứ tư).

– Nhìn lại các bước trên, ta thấy:

n_C = 5 = n_F + w_FC

= n_E + w_EF + w_FC

= n_A + w_AE + w_EF + w_FC

= w_AE + w_EF + w_FC

= l_AEFC.

Vậy AEFC là đường đi ngắn nhất từ A đến C, với độ dài bằng 5.

Do đó ta chọn phương án B.

Trong tập hợp số V, các cặp số là bội của 3 là:

• (1 và 2); (1 và 5);

• (2 và 4); (2 và 7);

• (3 và 6);

• (4 và 5);

• (5 và 7).

Ta vẽ đồ thị G có 7 đỉnh A₁; A₂; A₃; A₄; A₅; A₆; A₇ biểu diễn bảy số trong tập hợp số V.

Hai đỉnh biểu diễn hai số m và n được nối bằng một cạnh nếu m + n là bội của 3.

Ta có đồ thị G như sau: