10 bài tập Một số bài toán thực tế liên quan đến hình cầu có lời giải
55 người thi tuần này 4.6 526 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Câu 1
A. 7 234,56 cm2.
B. 1 808,64 cm2.
C. 150,72 cm2.
D. 452,16 cm2.
Lời giải
Đáp án đúng là: B
Bán kính của quả bóng là: 24 : 2 = 12 (cm).
Diện tích da cần dùng chính là tính diện tích bề mặt hình cầu.
Do đó, ta có diện tích da cần dùng để chế tạo bóng là: 4.3,14.122 = 1 808,64 (cm2).
Câu 2
A. 288 cm3.
B. 288π cm3.
C. 36 cm3.
D. 36π cm3.
Lời giải
Đáp án đúng là: B
Bán kính của quả pha lê đó là: \[\sqrt {144\pi :4\pi } \] = 6 (cm)
Thể tích của quả pha lê đó là: \[\frac{4}{3}\pi {.6^3} = 288\pi \] (cm3).
Sử dụng dữ liệu của bài toán dưới đây để trả lời Câu 3, 4.
Một tháp nước có bể chứa hình cầu, đường kính bên trong của bể đo được là 6 m.
Lời giải
Đáp án đúng là: D
Bán kính của tháp nước đó là; 6 : 2 = 3 (m).
Thể tích của tháp nước đó là: \[\frac{4}{3}\pi {.3^3} = 36\pi \] (m3).
Câu 4
A. 17,34 lít.
B. 16,87 lít.
C. 17,43 lít.
D. 16,78 lít.
Lời giải
Đáp án đúng là: A
Ta có, với π = 3,14 thì thể tích của bể đó là: 3,14.36 = 113,04 (m3)
Đổi 113,04 m3 = 113 040 lít.
Do đó, một ngày khu dân cư đó dùng hết số nước là:
113 040 : 5 = 22 608 (lít)
Suy ra một ngày bình quân mỗi người dùng hết số lít nước là:
22 608 : 1304 ≈ 17,34 (lít).
Câu 5
A. 116,8 cm2.
B. 118 cm2.
C. 117,8 cm2.
D. 118,7 cm2.
Lời giải
Đáp án đúng là: C
Gọi R là bán kính của quả bóng rổ (R > 0).
Ta có công thức tính diện tích bề mặt của quả bóng rổ hình cầu là:
S = 4πR2 (cm2).
Theo bài, diện tích bề mặt của quả bóng rổ khoảng 1 884,75 cm2 nên ta có:
4πR2 = 1 884,75 nên R2 = 1 884,75 : 4π = \[\frac{{7539}}{{16\pi }}\].
Suy ra R = \[\sqrt {\frac{{7539}}{{16\pi }}} = \frac{{\sqrt {7539\pi } }}{{4\pi }}\] (cm).
Vì bán kính của quả bóng rổ gấp khoảng 2 lần đường kính của quả bóng tennis nên đường kính của quả bóng tennis là: \[\frac{{\sqrt {7539\pi } }}{{4\pi }}\] : 2 = \[\frac{{\sqrt {7539\pi } }}{{8\pi }}\] (cm).
Do đó, bán kính của quả bóng tennis là: \[\frac{{\sqrt {7539\pi } }}{{8\pi }}\] : 2 = \[\frac{{\sqrt {7539\pi } }}{{16\pi }}\] (cm).
Suy ra diện tích bề mặt của quả bóng tennis đó là:
4π. \[{\left( {\frac{{\sqrt {7539\pi } }}{{16\pi }}} \right)^2} = \frac{{4\pi .7539\pi }}{{256{\pi ^2}}} = \frac{{7539}}{{64}} \approx 117,8\] (cm 2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 676 cm2.
B. 676π cm2.
C. \[\frac{{8788}}{3}\pi \] cm2.
D. \[\frac{{8788}}{3}\] cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
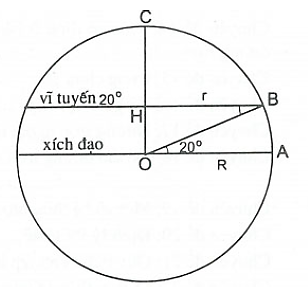
A. 2178,7 km.
B. 5985,8 km.
C. 2187,7 km.
D. 5958,8 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 332 500 đồng.
B. 665 000 đồng.
C. 664 110 đồng.
D. 332 055 đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.