Đề kiểm tra Vectơ trong không gian (có lời giải) - Đề 4
43 người thi tuần này 4.6 1.1 K lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Câu 2
Lời giải
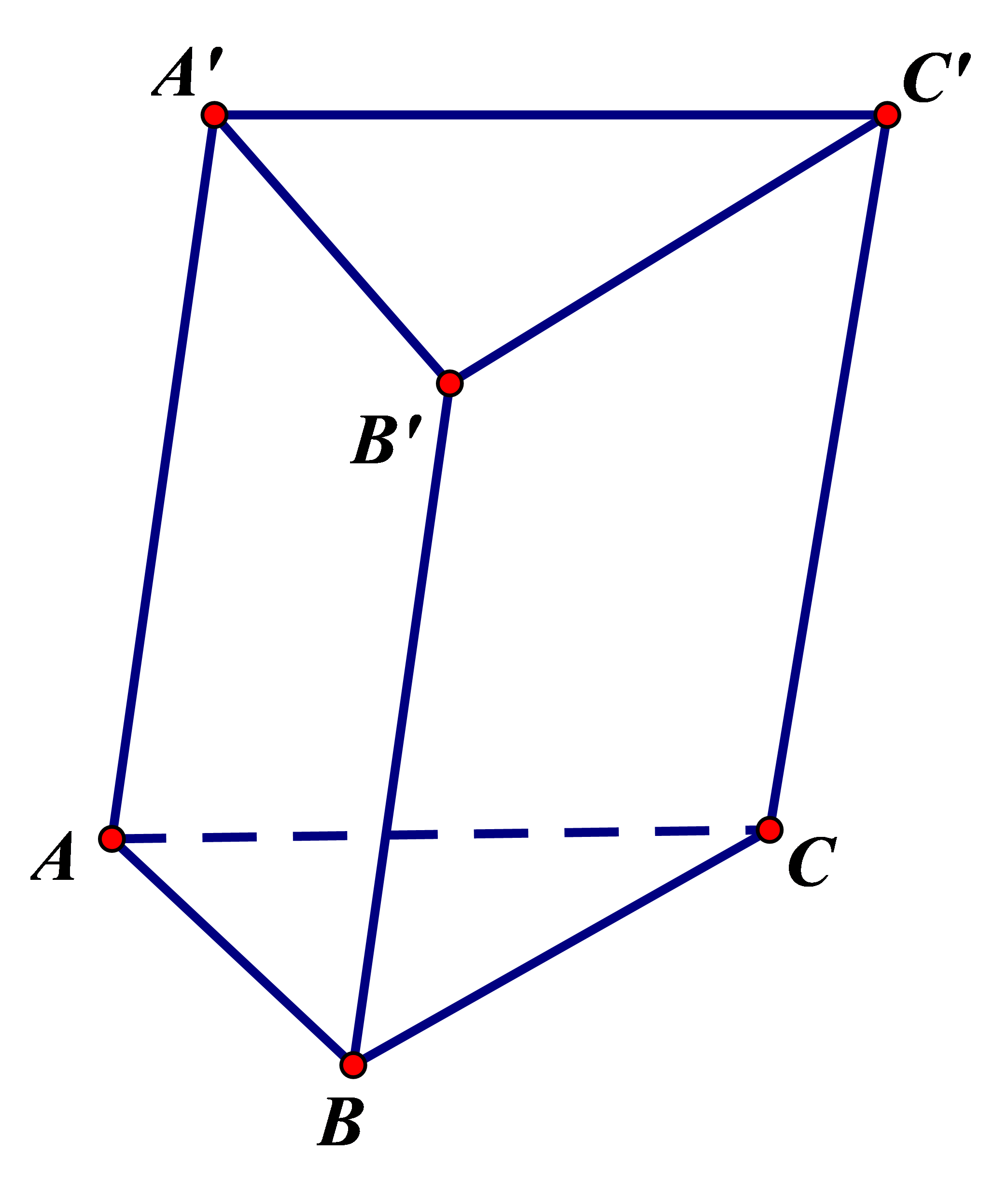
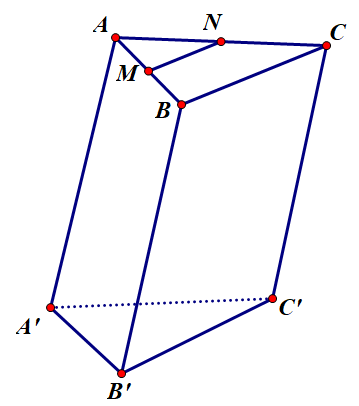
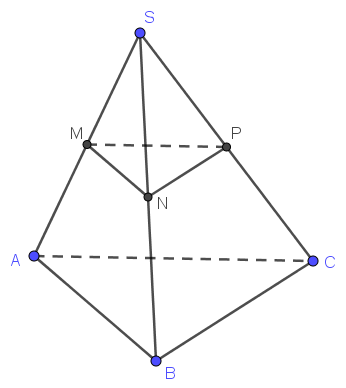
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN\) song song với \(BC\). Mà tứ giác \(BCC'B'\)là hình bình hành. Do đó \(MN\) song song với \(B'C'\). Vậy hai véc tơ \(\overrightarrow {MN} \)và \(\overrightarrow {B'C} '\)cùng hướng.
Lời giải
Đó là các véc tơ: \[\overrightarrow {DC} ,\,\overrightarrow {D'C'} ,\,\overrightarrow {A'B'} .\]
Câu 4
Lời giải
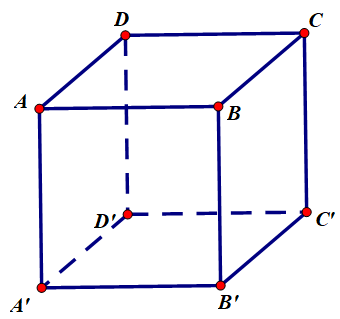
Xét hình hộp \(ABCD.A'B'C'D'\) ta có: \(\overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} = \overrightarrow {AC'} \).
Câu 5
Lời giải
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\), \(G\) lần lượt là trung điểm các đoạn thẳng \(AB\), \(CD\), \(AC\), \(BD\), \(AD\), \(BC\), \(MN\).
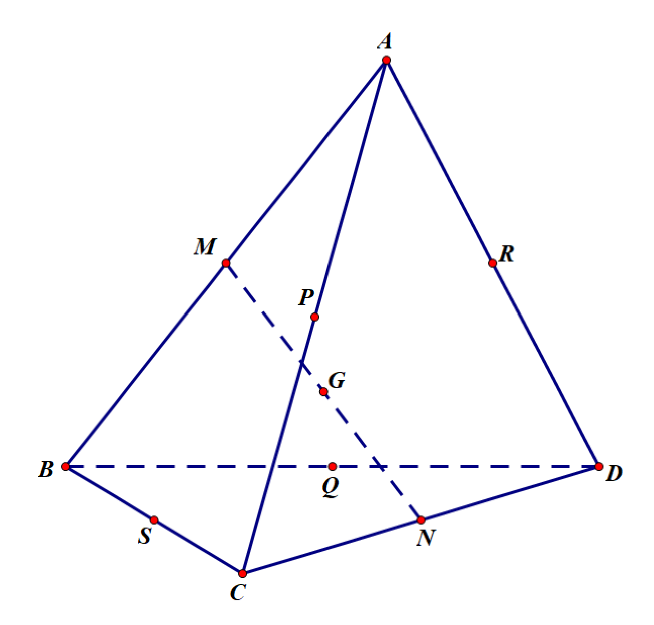
a) \(\overrightarrow {MR} = \overrightarrow {SN} \).
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
c) \(2\overrightarrow {PQ} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
d) \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right|\) nhỏ nhất khi và chỉ khi điểm \(I\) trùng với điểm \(G\).
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\), \(G\) lần lượt là trung điểm các đoạn thẳng \(AB\), \(CD\), \(AC\), \(BD\), \(AD\), \(BC\), \(MN\).

a) \(\overrightarrow {MR} = \overrightarrow {SN} \).
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
c) \(2\overrightarrow {PQ} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
d) \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right|\) nhỏ nhất khi và chỉ khi điểm \(I\) trùng với điểm \(G\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Cho hình hộp chữ nhật \[ABCD.EFGH\] có \[AB = AE = 2\], \[AD = 3\] và đặt \[\overrightarrow a = \overrightarrow {AB} ,\,\overrightarrow b = \overrightarrow {AD} ,\,\overrightarrow c = \overrightarrow {AE} \]. Lấy điểm \[M\] thỏa \[\overrightarrow {AM} = \frac{1}{5}\overrightarrow {AD} \] và điểm \[N\] thỏa \[\overrightarrow {EN} = \frac{2}{5}\overrightarrow {EC} \]. (tham khảo hình vẽ)
![Khi đó ta có a) \[\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759240659.png)
Khi đó ta có
a) \[\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \].
b) \[\overrightarrow {EN} = \frac{2}{5}\left( {\overrightarrow a - \overrightarrow b + \overrightarrow c } \right)\].
c) \[{\left( {m.\overrightarrow a + n.\overrightarrow b + n.\overrightarrow c } \right)^2} = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2}\] với \[m,\,n,\,p\] là các số thực.
d) \[MN = \frac{{\sqrt {61} }}{5}\].
Cho hình hộp chữ nhật \[ABCD.EFGH\] có \[AB = AE = 2\], \[AD = 3\] và đặt \[\overrightarrow a = \overrightarrow {AB} ,\,\overrightarrow b = \overrightarrow {AD} ,\,\overrightarrow c = \overrightarrow {AE} \]. Lấy điểm \[M\] thỏa \[\overrightarrow {AM} = \frac{1}{5}\overrightarrow {AD} \] và điểm \[N\] thỏa \[\overrightarrow {EN} = \frac{2}{5}\overrightarrow {EC} \]. (tham khảo hình vẽ)
![Khi đó ta có a) \[\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759240659.png)
Khi đó ta có
a) \[\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \].
b) \[\overrightarrow {EN} = \frac{2}{5}\left( {\overrightarrow a - \overrightarrow b + \overrightarrow c } \right)\].
c) \[{\left( {m.\overrightarrow a + n.\overrightarrow b + n.\overrightarrow c } \right)^2} = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2}\] với \[m,\,n,\,p\] là các số thực.
d) \[MN = \frac{{\sqrt {61} }}{5}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
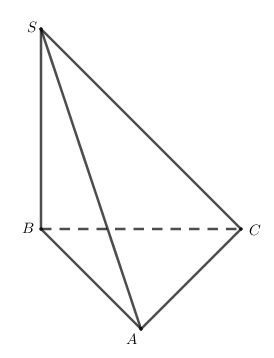
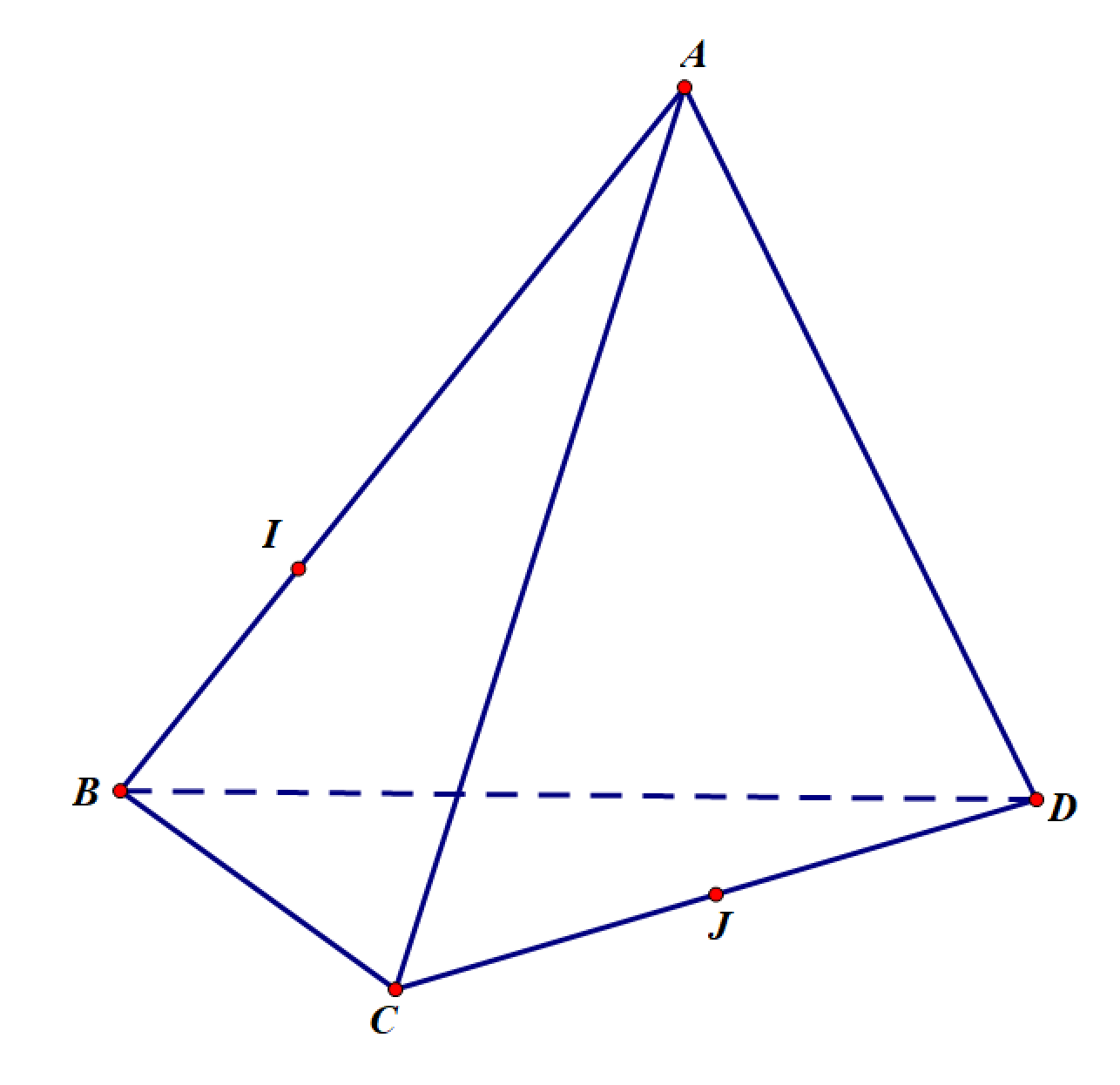
Cho tứ diện\(ABCD\), gọi \(I\),\(J\) lần lượt là trung điểm của \(AB\) và \(CD\).
1) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\].
2) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\].
3) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {AD} + \overrightarrow {BD} } \right)\].
4) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\].
Trong các đẳng thức trên có bao nhiêu đẳng thức đúng?
Cho tứ diện\(ABCD\), gọi \(I\),\(J\) lần lượt là trung điểm của \(AB\) và \(CD\).
1) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\].
2) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\].
3) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {AD} + \overrightarrow {BD} } \right)\].
4) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\].
Trong các đẳng thức trên có bao nhiêu đẳng thức đúng?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. [1] Cho tứ diện \(ABCD\) .Các véc tơ có điểm đầu là \(A\) và điểm cuối là các đỉnh còn lại của hình tứ diện là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759239860.png)
![Cho hình lăng trụ tam giác đều \[ABC.{A_1}{B_1}{C_1}\] có cạnh đáy bằng \[x\] và chiều cao bằng \[y\]. (tham khảo hình vẽ) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759240699.png)