Giải SBT Toán 10 CD Bài 6. Tích vô hướng của hai vectơ có đáp án

Lời giải

Đáp án đúng là A

Xét tam giác ABC, có:

\(\overrightarrow {BA} .\overrightarrow {CA} = \left( { - \overrightarrow {AB} } \right).\left( { - \overrightarrow {AC} } \right) = BA.CA.c{\rm{os}}\left( { - \overrightarrow {AB} , - \overrightarrow {AC} } \right)\)

= \(BA.CA.c{\rm{os}}\widehat {BAC}\)

= \(BA.CA.c{\rm{os}}\left( {\widehat {BAC}} \right)\)

Vậy chọn A.

Lời giải

Đáp án đúng là A

\(\overrightarrow {AB} .\overrightarrow {BC} = - \overrightarrow {BA} .\overrightarrow {BC} = - AB.BC.\cos \left( { - \overrightarrow {BA} ,\overrightarrow {BC} } \right)\)

= \( - AB.BC.\cos \left( {180^\circ - \widehat {ABC}} \right)\)

= \(AB.BC.\cos \widehat {ABC}\).

Vậy chọn A.

Lời giải

Đáp án đúng là D

Ta có: \(\overrightarrow {MA} .\overrightarrow {MB} = 0\)

⇒ \(\widehat {\left( {\overrightarrow {MA} ;\overrightarrow {MB} } \right)} = \widehat {AMB} = 90^\circ \)

Do đó tập hợp các điểm M thỏa mãn \(\widehat {AMB} = 90^\circ \) là đường tròn đường kính AB.

Lời giải

Đáp án đúng là B

Ta có: \(\overrightarrow {MN} .\overrightarrow {NM} = MN.MN.cos\left( {\overrightarrow {MN} ,\overrightarrow {NM} } \right) = MN.MN.cos180^\circ = - M{N^2}\)

Mà \(\overrightarrow {MN} .\overrightarrow {NM} = - 9\) nên – MN² = – 9 ⇔ MN² = 9 ⇔ MN = 3 (thỏa mãn) hoặc MN = – 3 (không thỏa mãn).

Vậy MN = 3.

Lời giải

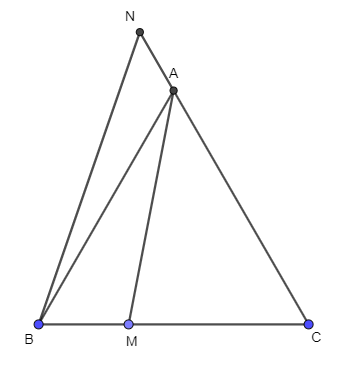
 Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.cos\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)

= \(AB.AC.\cos \widehat {BAC}\)

= \(a.a.\cos 60^\circ \)

= \(\frac{1}{2}{a^2}\)

\(\overrightarrow {AM} .\overrightarrow {BN} = \left( {\overrightarrow {AB} + \overrightarrow {BM} } \right).\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)

\( = \left( {\overrightarrow {AB} + \frac{1}{3}\overrightarrow {BC} } \right).\left( {\frac{1}{4}\overrightarrow {CA} - \overrightarrow {AB} } \right)\)

\( = \left[ {\overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)} \right].\left( { - \frac{1}{4}\overrightarrow {AC} - \overrightarrow {AB} } \right)\)

\( = \left( {\frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right).\left( { - \frac{1}{4}\overrightarrow {AC} - \overrightarrow {AB} } \right)\)

\( = - \frac{2}{3}\overrightarrow {AB} .\frac{1}{4}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} .\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} .\frac{1}{4}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AC} .\overrightarrow {AB} \)

\( = - \frac{1}{6}\overrightarrow {AB} .\overrightarrow {AC} - \frac{2}{3}{\overrightarrow {AB} ^2} - \frac{1}{{12}}{\overrightarrow {AC} ^2} - \frac{1}{3}\overrightarrow {AC} .\overrightarrow {AB} \)

\( = - \frac{1}{6}.\frac{1}{2}{a^2} - \frac{2}{3}.{a^2} - \frac{1}{{12}}.{a^2} - \frac{1}{3}.\frac{1}{2}{a^2}\)

\( = - \frac{1}{{12}}{a^2} - \frac{2}{3}.{a^2} - \frac{1}{{12}}.{a^2} - \frac{1}{6}{a^2}\)

\( = - {a^2}\).