10 bài tập Một số bài toán thực tế liên quan Bài 3. Đường tiệm cận của đồ thị hàm số (có lời giải)
4.6 0 lượt thi 10 câu hỏi 45 phút
🔥 Đề thi HOT:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải (P1)
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Tập xác định: D = ℝ.
Ta có: \[\mathop {\lim }\limits_{x \to - \infty } \] [\[55 - \frac{1}{2}\sqrt {{x^2} + 144} \]−(\[55 - \frac{1}{2}x\])] = 0
Tương tự ta cũng có: \[\mathop {\lim }\limits_{x \to + \infty } \] [\[55 - \frac{1}{2}\sqrt {{x^2} + 144} \]−(\[55 - \frac{1}{2}x\])] = 0
Do đó y = \[55 - \frac{1}{2}x\] là tiệm cận xiên của đồ thị hàm số y = \[55 - \frac{1}{2}\sqrt {{x^2} + 144} \].
Lời giải
Có \(\mathop {\lim }\limits_{x \to {0^ + }} C(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{50x + 2000}}{x} = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} C(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{50x + 2000}}{x} = - \infty \)
Vậy \(x = 0\) là tiệm cận đứng của đồ thị hàm số.
Có \(\mathop {\lim }\limits_{x \to + \infty } C(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50;\mathop {\lim }\limits_{x \to - \infty } C(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\).
Vậy \({\rm{y}} = 50\) là tiệm cận ngang của đồ thị hàm số.
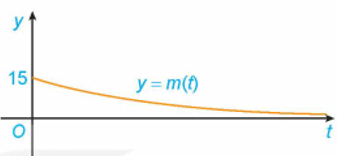
Lời giải
Do đó là tiệm cận ngang của đồ thị hàm số và hàm số không có tiệm cận đứng, tiệm cận xiên.
Lời giải
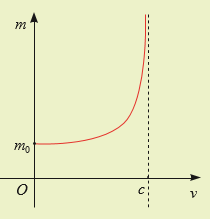
Tập xác định: \({\rm{D}} = (0;{\rm{c}}]\).
Có \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = + \infty ;\mathop {\lim }\limits_{v \to c} m(v) = \mathop {\lim }\limits_{v \to c} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = + \infty \)
Do đó \(v = c\) là tiệm cận đứng của đồ thị hàm số.
Hàm số không có tiệm cận ngang.
Khi hạt di chuyến với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt tiến gần tới vô cùng.
Trên hình điều này được thế hiện đường cong biếu diễn \(m(v)\) sẽ tiến dần đến vô cùng khi \(v \to c\). Điều này cho thấy rẳng khối lượng của hạt sẽ tăng tới vô cùng khi tốc độ di chuyến của nó tiến gân tốc độ ánh sáng.Lời giải
a) Sau 1 phút, ta có: khối lượng muối trong bể là 25 . 30 . t = 750t (gam); thể tích của lượng nước trong bể là 5 000 + 25t (lít). Vậy nồng độ muối sau 1 phút là \[f(t) = \frac{{750t}}{{5000 + 25t}} = \frac{{30t}}{{200 + t}}\] (gam/lít).
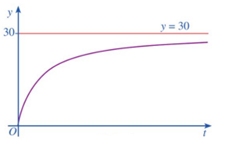
b) Ta có: \[\mathop {\lim }\limits_{t \to + \infty } f(t) = \mathop {\lim }\limits_{t \to + \infty } \frac{{30t}}{{200 + t}} = \mathop {\lim }\limits_{t \to + \infty } \left( {30 - \frac{{6000}}{{200 + t}}} \right) = 30\]
Vậy đường thẳng y = 30 là tiệm cận ngang của đồ thị hàm số f(t).
c) Ta có đồ thị hàm số y = f(t) nhận đường thẳng y = 30 làm tiệm cận ngang, tức là khi t càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Lúc đó, nồng độ muối trong bể sẽ gần như bằng nồng độ muối trong nước muối được bơm vào bể.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.