Giải SBT Toán 10 Bài tập cuối chương 4 có đáp án

Đáp án đúng là: A

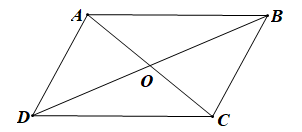
Các vectơ khác vectơ - không và cùng phương với \(\overrightarrow {AC} \) là: \[\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {AO} ,\overrightarrow {OA} ,\overrightarrow {OC} ,\overrightarrow {CO} .\]

Vậy có 6 vectơ khác vectơ - không và cùng phương với \(\overrightarrow {AC} .\)

Vậy ta chọn phương án A.

Đáp án đúng là: C

Vì B nằm giữa A và C nên ta có:

• \(\overrightarrow {AB} \) và \[\overrightarrow {CB} \] ngược hướng. Do đó phương án A sai.

• \(\overrightarrow {CA} \) và \(\overrightarrow {BC} \) ngược hướng. Do đó phương án B sai.

• \[\overrightarrow {AB} \] và \(\overrightarrow {AC} \) cùng hướng. Do đó phương án C đúng.

• \(\overrightarrow {AC} \) và \(\overrightarrow {BA} \) ngược hướng. Do đó phương án D sai.

Vậy ta chọn phương án C.

Đáp án đúng là: C

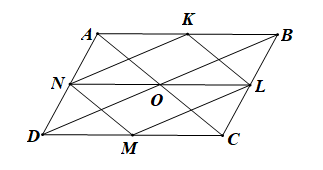
Vì ABCD là hình bình hành nên AB // CD và AB = CD.

Lại có K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA

Nên AK = KB = DM = MC và NL // AB // CD

Do đó ABLN là hình bình hành (do AB // NL và AN // BL)

Suy ra AB = NL = CD

Mà O là tâm hình bình hành nên O là trung điểm của AC và BD

Do đó đường trung bình NL đi qua O

Và NO = OL = \(\frac{1}{2}NL = \frac{1}{2}AB = \frac{1}{2}CD\)

Suy ra AK = KB = NO = OL = DM = MC.

Khi đó các vectơ bằng vectơ \(\overrightarrow {AK} \) là: \(\overrightarrow {KB} ,\overrightarrow {OL} ,\overrightarrow {DM} ,\overrightarrow {MC} .\)

Vậy có 4 vectơ bằng vectơ \(\overrightarrow {AK} .\)

Ta chọn phương án C.

Đáp án đúng là: D

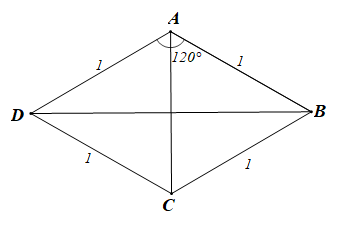
• Xét phương án A:

Vì ABCD là hình thoi nên AB // CD suy ra \(\overrightarrow {AB} = \overrightarrow {DC} .\)

Do đó phương án A là sai.

• Xét phương án B:

Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau.

Khi đó \(\overrightarrow {BD} \bot \overrightarrow {AC} \) nên \[\overrightarrow {BD} \ne \overrightarrow {AC} .\]

Do đó phương án B là sai.

• Xét phương án C:

Vì ABCD là hình thoi có cạnh bằng 1 nên AD = AB = 1.

Xét ABD có AB = AD = 1 và \(\widehat {DAB} = 120^\circ ,\) áp dụng định lí cosin ta có:

BD² = AD² + AB² – 2.AD.AB.cos\(\widehat {DAB}\)

BD² = 1² + 1² – 2.1.1.cos120°

BD² = 3

BD = \(\sqrt 3 \)

Khi đó \(\left| {\overrightarrow {BD} } \right| = BD = \sqrt 3 .\)

Do đó phương án C là sai.

• Xét phương án D:

Vì ABCD là hình thoi có cạnh bằng 1 nên AD = CD = 1 .

Mặt khác \(\widehat {DAB} = 120^\circ \) nên \(\widehat {ADC} = 180^\circ - \widehat {DAB} = 180^\circ - 120^\circ = 60^\circ \)

Tam giác ADC có AD = DC nên là tam giác cân lại có \(\widehat {ADC} = 60^\circ \)

Suy ra ADC là tam giác đều

AC = AD = CD = 1.

Khi đó \(\left| {\overrightarrow {AC} } \right| = AC = 1.\)

Do đó phương án D là đúng.

Đáp án đúng là: A

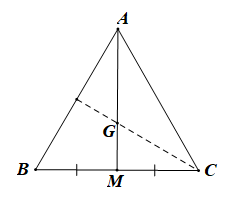
Tam giác ABC đều có cạnh bằng 3 nên AB = AC = 3 và \(\widehat {BAC} = 60^\circ .\)

Gọi M là trung điểm của BC.

Khi đó ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)

\( \Rightarrow {\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)^2} = {\left( {2\overrightarrow {AM} } \right)^2}\)

\( \Rightarrow A{B^2} + 2.\overrightarrow {AB} .\overrightarrow {AC} + A{C^2} = 4A{M^2}\)

\( \Rightarrow A{B^2} + 2.AB.AC.c{\rm{os}}\widehat {BAC} + A{C^2} = 4A{M^2}\)

3² + 2.3.3.cos60° + 3² = 4.AM²

4.AM² = 27

AM² = \(\frac{{27}}{4}\)

AM = \(\sqrt {\frac{{27}}{4}} = \frac{{3\sqrt 3 }}{2}\)

Vì G là trọng tâm tam giác ABC nên AG = \(\frac{2}{3}\)AM

AG = \(\frac{2}{3}.\frac{{3\sqrt 3 }}{2} = \sqrt 3 .\)

Khi đó \(\left| {\overrightarrow {AG} } \right| = AG = \sqrt 3 .\)

Vậy ta chọn phương án A.

Đáp án đúng là: B

Gọi D là điểm thỏa mãn \(\overrightarrow {AB} = \overrightarrow {CD} \)

Khi đó CD // AB và CD = AB(1)

Ta có: \[\overrightarrow {CB} + \overrightarrow {AB} = \overrightarrow {CB} + \overrightarrow {CD} \]

Gọi E là điểm thỏa mãn BCDE là hình bình hành.

Khi đó CD // BE và CD = BE(2)

Từ (1) và (2) ta có: AB ≡ BE và AB = BE

Do đó B là trung điểm của AE

AE = 2AB = 2.3 = 6.

Xét tam giác ACE vuông tại A, theo định lí Pythagore ta có:

CE² = AC² + AE² = 4² + 6² = 52

CE = \(\sqrt {52} = 2\sqrt {13} .\)

Vì ABCD là hình bình hành nên \[\overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CE} \] (quy tắc hình bình hành)

\( \Rightarrow \left| {\overrightarrow {CB} + \overrightarrow {AB} } \right| = \left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CE} } \right| = CE = 2\sqrt {13} .\)

Vậy ta chọn phương án B.

Đáp án đúng là: C

Xét ABC có AB = 2, BC = 4 và \(\widehat {ABC} = 60^\circ .\)

Khi đó tam giác ABC là tam giác vuông tại A.

\( \Rightarrow \widehat {BAC} = 90^\circ .\)

Ta có: \(\overrightarrow {AC} - \overrightarrow {BA} = \overrightarrow {AC} + \overrightarrow {AB} \)

Gọi D là điểm thỏa mãn ABDC là hình bình hành

Khi đó \(\overrightarrow {AC} - \overrightarrow {BA} = \overrightarrow {AC} + \overrightarrow {AB} = \overrightarrow {AD} \)

\[ \Rightarrow \left| {\overrightarrow {AC} - \overrightarrow {BA} } \right| = \left| {\overrightarrow {AD} } \right| = AD\]

Hình bình hành ABDC có \(\widehat {BAC} = 90^\circ \) nên là hình chữ nhật.

Do đó AD = BC (hai đường chéo bằng nhau)

\[ \Rightarrow \left| {\overrightarrow {AC} - \overrightarrow {BA} } \right| = AD = BC = 4.\]

Vậy ta chọn phương án C.

Đáp án đúng là: D

Ta có: \(\overrightarrow {IB} + 2\overrightarrow {IC} = \overrightarrow 0 \Rightarrow \overrightarrow {IB} = - 2\overrightarrow {IC} \)

Khi đó \(\overrightarrow {IB} \) và \(\overrightarrow {IC} \) là hai vectơ cùng phương, ngược hướng và IB = 2IC.

Khi đó điểm I nằm giữa hai điểm B và C sao cho IB = 2IC.

Gọi M là trung điểm của BI.

Khi đó M là trung điểm của BI, I là trung điểm của MC.

Vì I là trung điểm của MC nên ta có:

\(2\overrightarrow {AI} = \overrightarrow {AM} + \overrightarrow {AC} \)(1)

Vì M là trung điểm của BI nên ta có:

\(2\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AI} \)

\( \Rightarrow \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} \)(2)

Thay (2) vào (1) ta được:

\(2\overrightarrow {AI} = \overrightarrow {AM} + \overrightarrow {AC} \)

\( \Rightarrow 2\overrightarrow {AI} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} } \right) + \overrightarrow {AC} \)

\( \Rightarrow 2\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} + \overrightarrow {AC} \)

\( \Rightarrow 2\overrightarrow {AI} - \frac{1}{2}\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AB} + \overrightarrow {AC} \)

\( \Rightarrow \frac{3}{2}\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AB} + \overrightarrow {AC} \)

\( \Rightarrow \overrightarrow {AI} = \frac{2}{3}.\left( {\frac{1}{2}\overrightarrow {AB} + \overrightarrow {AC} } \right)\)

\( \Rightarrow \overrightarrow {AI} = \frac{{\overrightarrow {AB} + 2\overrightarrow {AC} }}{3}\)

Vậy ta chọn phương án D.