Bộ 5 đề thi giữa kì 1 Toán 11 Cánh diều cấu trúc mới có đáp án - Đề 3
26 người thi tuần này 4.6 667 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 6 (có lời giải) - Đề 1
Đề kiểm tra Phương trình – bất phương trình mũ và lôgarit (có lời giải) - Đề 3
Đề kiểm tra Phương trình – bất phương trình mũ và lôgarit (có lời giải) - Đề 2
Đề kiểm tra Phương trình – bất phương trình mũ và lôgarit (có lời giải) - Đề 1
Danh sách câu hỏi:
Câu 1
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, học sinh chỉ chọn một phương án
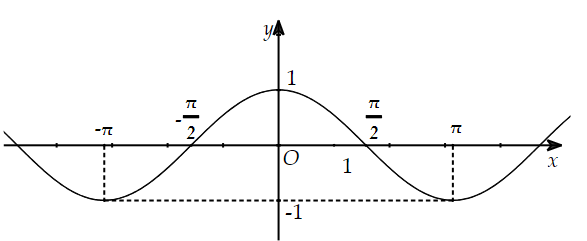
Đường cong dưới đây là đồ thị hàm số của hàm số nào trong các đáp án A, B, C, D?
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Đồ thị đối xứng qua trục \[Oy\] nên đó là hàm số \[y = \cos x.\]
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Ta có: \[\sin x = \frac{4}{5}\] với \[\frac{\pi }{2} < x < \pi \] thì \[x\] thuộc góc phần tư thứ II.
Do đó, \[\cos x < 0\].
Vậy \[\cos x = - \sqrt {1 - {{\sin }^2}x} = - \frac{3}{5}\].
Câu 3
Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây.
![Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây. A. \[ - 300^\circ .\] B. \[510^\circ .\] C. \[60^\circ .\] D. \[ - 420^\circ .\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1760799467.png)
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \[\left( {Ou,Ov} \right) = - \left( {360^\circ - 60^\circ } \right) = - 300^\circ \].
Câu 4
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Điều kiện: \[1 - \cos x \ne 0\] \[ \Leftrightarrow \cos x \ne 1\]\[ \Leftrightarrow x \ne k2\pi ,{\rm{ }}k \in \mathbb{Z}.\]
Vậy tập xác định của hàm số \[y = \frac{{\sin x}}{{1 - \cos x}}\] là \[D = \mathbb{R}\backslash \left\{ {k2\pi |k \in \mathbb{Z}} \right\}.\]
Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \[2\sin x - \sqrt 3 = 0\]
\[ \Leftrightarrow \sin x = \frac{{\sqrt 3 }}{2}\] \[ \Leftrightarrow \sin x = \sin \left( {\frac{\pi }{3}} \right)\] \[ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}.\]
Câu 6
A. \[1; - 2; - 4; - 6; - 8.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Cho hình chóp \[S.ABCD\], biết \[AB\] cắt \[CD\] tại \[E\], \[AC\] cắt \[BD\] tại \[F\] trong mặt phẳng đáy. Xét tính đúng sai của các khẳng định sau:
a) Đường thẳng \[FE\] nằm trong mặt phẳng \[\left( {ABCD} \right).\]
b) \[AB\] là giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {ABCD} \right).\]
c) \[SF\] là giao điểm của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\], \[SE\] là giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right).\]
d) Gọi \[G = FE \cap AD\]. Khi đó, \[SG\] là giao tuyến của mặt phẳng \[\left( {SFE} \right)\] và mặt phẳng \[\left( {SAD} \right)\].
Cho hình chóp \[S.ABCD\], biết \[AB\] cắt \[CD\] tại \[E\], \[AC\] cắt \[BD\] tại \[F\] trong mặt phẳng đáy. Xét tính đúng sai của các khẳng định sau:
a) Đường thẳng \[FE\] nằm trong mặt phẳng \[\left( {ABCD} \right).\]
b) \[AB\] là giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {ABCD} \right).\]
c) \[SF\] là giao điểm của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\], \[SE\] là giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right).\]
d) Gọi \[G = FE \cap AD\]. Khi đó, \[SG\] là giao tuyến của mặt phẳng \[\left( {SFE} \right)\] và mặt phẳng \[\left( {SAD} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một cây cầu có dạng cung \[OA\] là một phần của đ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/23-1760800085.png)