Đề cương ôn tập giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Bài 5. Tích của một số với một vectơ
23 người thi tuần này 4.6 1 K lượt thi 11 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 3
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 2
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) - Đề 1
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 3
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
\[0.\overrightarrow a = \overrightarrow 0 \]. Chọn C.
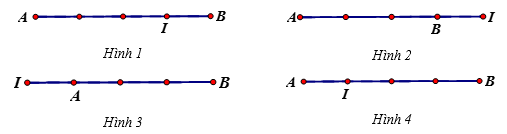
Câu 2
A. Hình 1.
Lời giải
Ta có\[\overrightarrow {IB} + 3\overrightarrow {IA} = \overrightarrow 0 \Leftrightarrow \overrightarrow {IB} = - 3\overrightarrow {IA} \].
Do đó \[IB = 3.IA\];\[\overrightarrow {IA} \] và \[\overrightarrow {IB} \] ngược hướng. Chọn Hình 4. Chọn D.
Câu 3
Lời giải
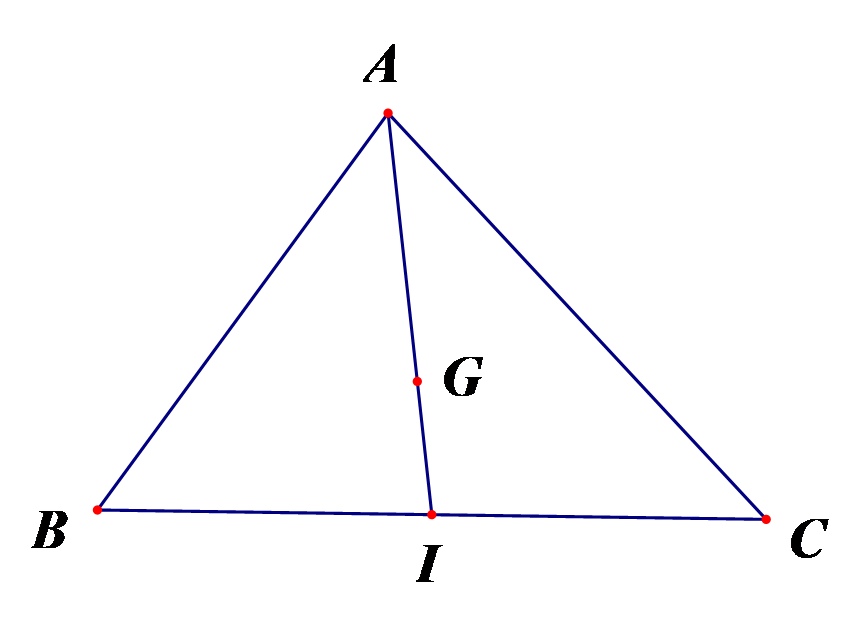
Vì \[I\] là trung điểm của \[BC\] suy ra \[\overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 .\]
Ta có \[\left\{ \begin{array}{l}\overrightarrow {GB} = \overrightarrow {GI} + \overrightarrow {IB} \\\overrightarrow {GC} = \overrightarrow {GI} + \overrightarrow {IC} \end{array} \right. \Rightarrow \overrightarrow {GB} + \overrightarrow {GC} = \underbrace {\overrightarrow {IB} + \overrightarrow {IC} }_{\overrightarrow 0 } + 2\,\overrightarrow {GI} = 2\,\overrightarrow {GI} .\] Chọn C.
Câu 4
Lời giải

Vì \(M\) là trung điểm \(BC\) nên \[\overrightarrow {IB} + \overrightarrow {IC} = 2\overrightarrow {IM} .\]
Mặt khác \(I\) là trung điểm \(AM\) nên \(\overrightarrow {IA} + \overrightarrow {IM} = \overrightarrow 0 .\)
Suy ra \[\overrightarrow {IB} + \overrightarrow {IC} + 2\overrightarrow {IA} = 2\overrightarrow {IM} + 2\overrightarrow {IA} = 2\left( {\overrightarrow {IM} + \overrightarrow {IA} } \right) = \overrightarrow 0 .\] Chọn B.
Câu 5
Lời giải
Gọi \[G\] là trọng tâm của tam giác \[ABC\], ta có \[\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \].
Thay vào ta được : \[\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 5 \Leftrightarrow \left| {3\overrightarrow {MG} } \right| = 5 \Leftrightarrow MG = \frac{5}{3}\], hay tập hợp các điểm \[M\]là đường tròn có tâm là trọng tâm của tam giác \[ABC\] và bán kính bằng \[\frac{5}{3}\] . Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.