Đề cương ôn tập giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Bài 2: Hệ bất phương trình bậc nhất hai ẩn
25 người thi tuần này 4.6 1 K lượt thi 18 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 3
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 2
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) - Đề 1
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 3
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Thay cặp số \(\left( {1\,;0} \right)\) vào hệ bất phương trình ta được \(\left\{ {\begin{array}{*{20}{c}}{1 + 0 > - 3}\\{ - 1 + 2.0 < 3}\end{array}} \right.\) (luôn đúng).
Do đó cặp số \(\left( {1\,;0} \right)\) là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y > - 3}\\{ - x + 2y < 3}\end{array}} \right.\). Chọn A.
Câu 2
Lời giải
Thay \(\left( { - 1\,;1} \right)\) vào bất phương trình thứ hai của hệ ta được \( - 1 - 2.1 = - 3 > - 2\) (vô lí).
Do đó cặp số \(\left( { - 1\,;1} \right)\) không là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 3}\\{x - 2y > - 2}\end{array}} \right.\). Chọn C.
Câu 3
Lời giải
Thay tọa độ điểm \(M\left( {0\,;1} \right)\) vào hệ bất phương trình ta có: \[\left\{ \begin{array}{l}0 + 3.1 - 2 \ge 0\\2.0 + 1 + 1 > 0\end{array} \right.\] (luôn đúng).
Do đó điểm \(M\left( {0\,;1} \right)\) thuộc miền nghiệm của hệ bất phương trình. Chọn D.
Câu 4
Lời giải
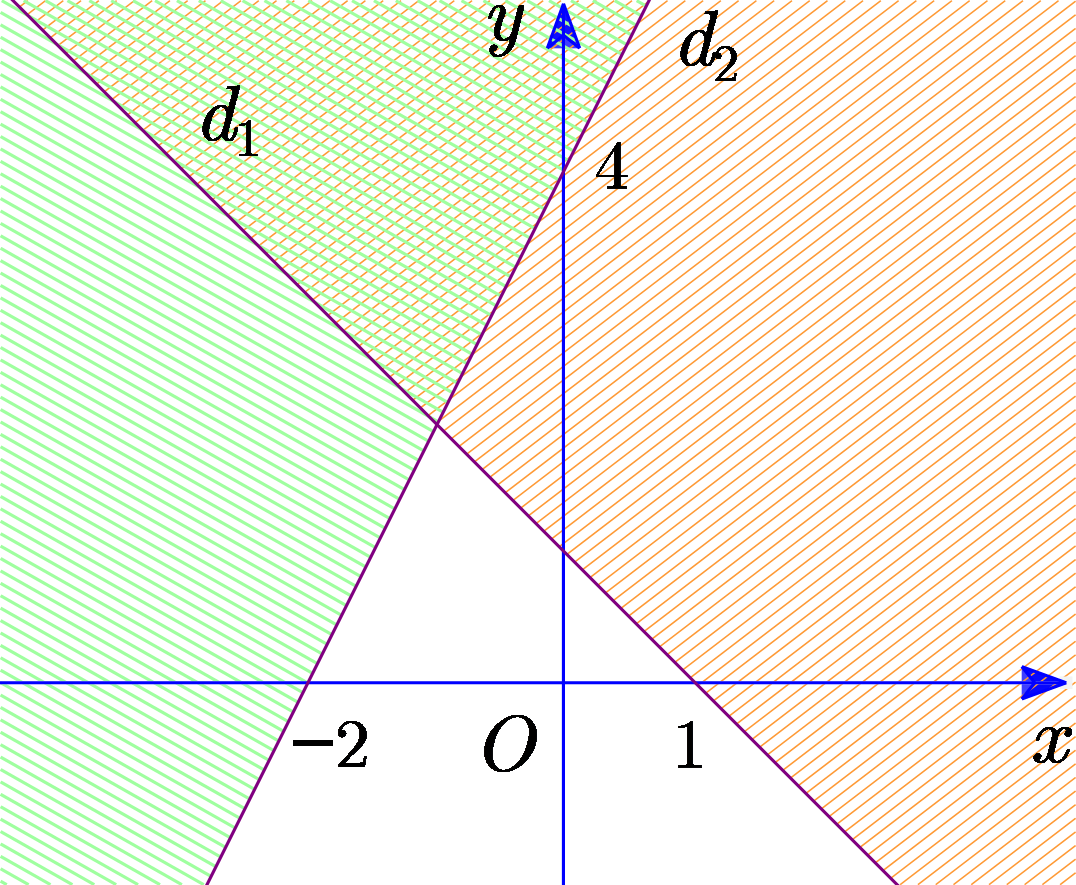
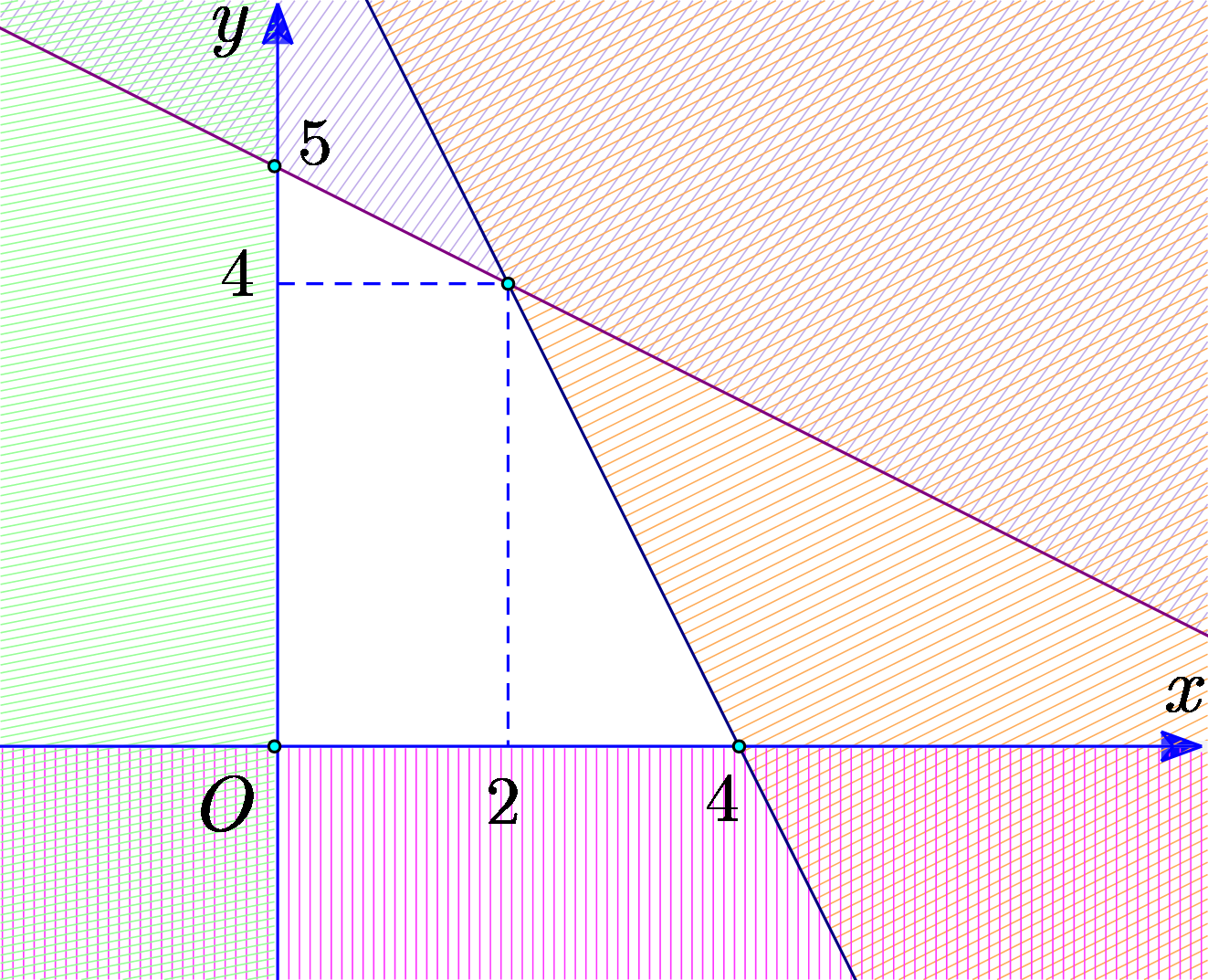
Đường thẳng d1 đi qua điểm (1; 0) và (0; 1) có phương trình là \(x + y - 1 = 0\).
Vì O(0; 0) không thuộc d1 thuộc vào miền nghiệm nên thay (0; 0) vào d1 ta có \( - 1 < 0\).
Suy ra \(x + y - 1 \le 0\).
Đường thẳng d2 đi qua điểm (−2; 0) và (0; 4) có phương trình \(2x - y + 4 = 0\).
Vì O(0; 0) không thuộc d2 thuộc miền nghiệm nên thay (0; 0) vào d2 ta có 4 > 0.
Suy ra \(2x - y + 4 \ge 0\).
Vậy miền không bị gạch chéo là miền nghiệm của bất phương trình \(\left\{ \begin{array}{l}x + y - 1 \le 0\\2x - y + 4 \ge 0\end{array} \right.\). Chọn C.
Câu 5
Lời giải
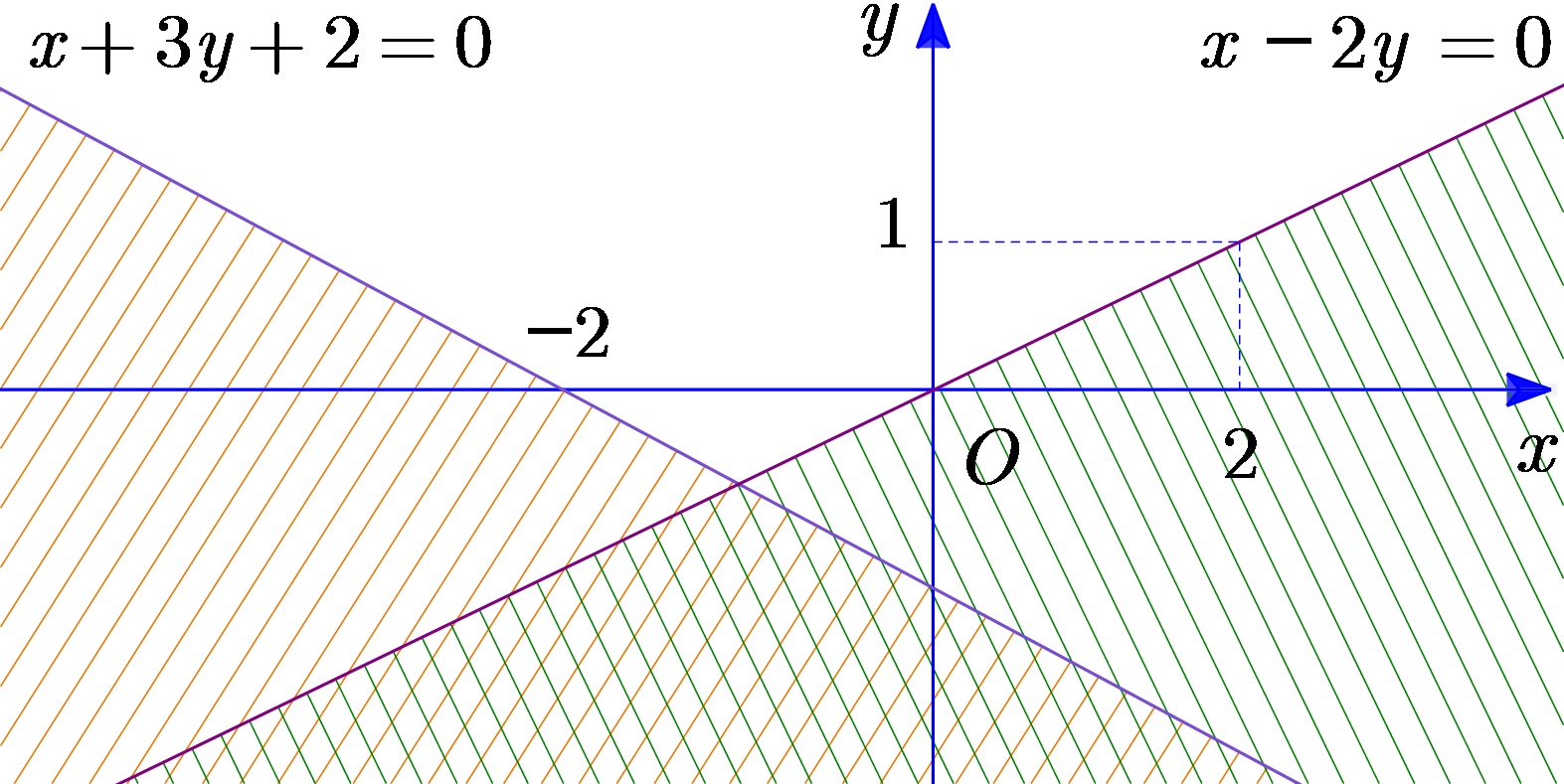
Ta chọn điểm (−1; 1) thuộc miền nghiệm của hệ bất phương trình thay vào lần lượt các phương trình đường thẳng ta được:
\(\left\{ \begin{array}{l} - 1 - 2.1 = - 3 < 0\\ - 1 + 3.1 + 2 = 4 > 0\end{array} \right.\).
Suy ra hệ bất phương trình là \(\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \ge - 2\end{array} \right.\). Chọn A.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(\left\{ \begin{array}{l}2x - y - 2 < 0\\x + y < 2\\6x - y + 2 > 0\end{array} \right.\).
B. \(\left\{ \begin{array}{l}2x - y - 2 < 0\\x + y < 2\\6x - y + 2 < 0\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\) (I).
a) \(\left( {0;3} \right)\) là một nghiệm của (I).
b) Miền nghiệm của (I) chứa điểm (1; 3).
c) \(M\left( {x;y} \right)\) thuộc miền nghiệm của (I) thì \(2y - x \le 7\).
d) Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định là 1.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\) (I).
a) \(\left( {0;3} \right)\) là một nghiệm của (I).
b) Miền nghiệm của (I) chứa điểm (1; 3).
c) \(M\left( {x;y} \right)\) thuộc miền nghiệm của (I) thì \(2y - x \le 7\).
d) Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định là 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.