Bộ 19 đề thi Giữa kì 1 Toán 11 Cánh diều có đáp án - Đề 5
21 người thi tuần này 4.6 1.8 K lượt thi 19 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \(\left\{ {k\pi ,k \in \mathbb{Z};\frac{\pi }{4} + l\frac{\pi }{2}\,,\,l \in \mathbb{Z}} \right\}\).
Lời giải
Chọn A
\( \Leftrightarrow \left[ \begin{array}{l}3x = x + k2\pi \\3x = \pi - x + l2\pi \end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \frac{\pi }{4} + \frac{{l\pi }}{2}\end{array} \right.,\)\(k \in \mathbb{Z},l \in \mathbb{Z}\).
Vậy tập nghiệm của phương trình là: \(\left\{ {k\pi ,k \in \mathbb{Z};\frac{\pi }{4} + l\frac{\pi }{2}\,,\,l \in \mathbb{Z}} \right\}\)
Câu 2
Lời giải
Chọn C
Hai đường thẳng phân biệt \[a\] và \[b\]trong không gian có những vị trí tương đối sau:
Hai đường thẳng phân biệt \[a\] và \(y = \frac{{2 - x}}{{9 - {x^2}}}\) cùng nằm trong một mặt phẳng thì chúng có thể song song hoặc cắt nhau
Hai đường thẳng phân biệt \[a\] và \[b\] không cùng nằm trong một mặt phẳng thì chúng chéo nhau
Vậy chúng có 3 vị trí tương đối là song song hoặc cắt nhau hoặc chéo nhau.
Câu 3
Lời giải
Chọn A
Câu 4
Lời giải
Chọn C
Ta có: \(\cos 2a = 2{\cos ^2}a - 1\) nên A sai.
Và: \(\cos 2a = 1 - 2{\sin ^2}a \Leftrightarrow 2{\sin ^2}a = 1 - \cos 2a\) nên B đúng.
Các đáp án C và D hiển nhiên đúng.
Câu 5
Lời giải
Chọn A
Điều kiện \(2\cos x - 1 \ne 0 \Leftrightarrow \cos x \ne \frac{1}{2} \Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{3} + k2\pi \\x \ne \frac{{5\pi }}{3} + k2\pi \end{array} \right.\), \[k \in \mathbb{Z}\].
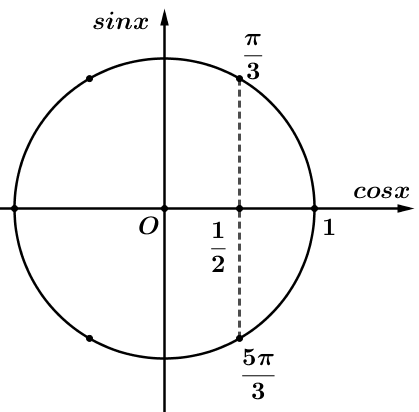
Vậy tập xác định của hàm số là \[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{3} + k2\pi ,\frac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\].
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[\frac{{25\pi }}{{12}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.