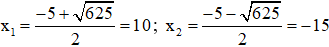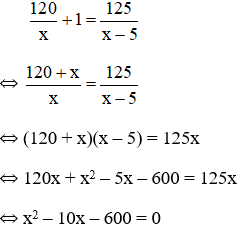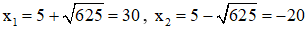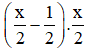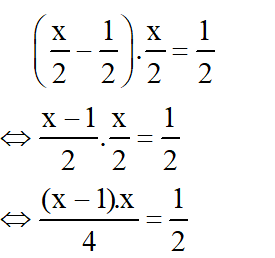Bài 8: Giải bài toán bằng cách lập phương trình
29 người thi tuần này 4.6 40.9 K lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Gọi chiều dài của mảnh vườn là x (m) (x > 4)
Chiều rộng của mảnh vườn là x – 4 (m)
Diện tích của mảnh vườn là 320 m2 nên ta có phương trình:
x(x - 4) = 320
⇔ x2 - 4x - 320 = 0
Δ' = 22 + 320 = 324, √(Δ') = 18
x1 = 2 + 18 = 20; x2 = 2 - 18 = -16
x2 = -16 không thỏa mãn điều kiện của ẩn
Vậy chiều dài của mảnh vườn là 20m
Chiều rộng của mảnh vườn là 16 m
Lời giải
Gọi x là số mà một bạn chọn
⇒ số còn lại là x + 5.
⇒ tích của hai số là x(x+5).
Theo đề bài ta có phương trình:
x(x+ 5) = 150
⇔ x2 + 5x = 150
⇔ x2 + 5x – 150 = 0 (*)
Phương trình (*) có: a = 1; b = 5; c = -150
⇒ Δ = 52 – 4.1.(-150) = 625 > 0
⇒ (*) có hai nghiệm
Vậy hai số mà Minh và Lan phải chọn là 10 và 15.
Hoặc hai số mà hai bạn chọn là -10 và –15.
Lời giải
Gọi lãi suất cho vay là : x (x > 0).
Lãi suất sau năm đầu tiên là : 2 000 000.x
Số tiền bác phải trả sau năm đầu tiên là :
2 000 000 + 2 000 000. x = 2 000 000.(1 + x)
Số tiền trên được tính là vốn của năm thứ hai.
Số tiền lãi của năm thứ hai là : 2 000 000.(1 + x).x
Số tiền vốn và lãi phải trả sau năm thứ hai là:
2 000 000.(1 + x) + 2 000 000.(1 + x). x = 2 000 000.(1 + x)2
Lời giải
Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5).
⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).
Thời gian đi là: 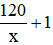
Quãng đường về là: 120 + 5 = 125 km
Thời gian về là: 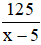
Theo bài ra ta có phương trình:
Có a = 1; b = -10; c = -600 ⇒ Δ’ = (-5)2 – 1.(-600) = 625
Phương trình có hai nghiệm phân biệt:
Trong hai nghiệm chỉ có nghiệm x = 30 thỏa mãn điều kiện.
Vậy vận tốc xuồng lúc đi là 30 km/h.
Lời giải
Gọi số cần tìm là x.
+ Một nửa của x trừ đi một nửa đơn vị rồi nhân với một nửa của x là:
Theo bài ra ta có phương trình:
Có a = 1; b = -1; c = -2
⇒ a – b + c = 1 – (-1) – 2 = 0
⇒ Phương trình có hai nghiệm x1 = -1; x2 = 2.
Vậy số cần tìm là -1 hoặc 2.
Kiến thức áp dụng