10 Bài tập Ứng dụng hệ bất phương trình bậc nhất hai ẩn để giải bài toán kinh tế (có lời giải)
63 người thi tuần này 4.6 413 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Câu 1
A. 20 kg sản phẩm loại I và 40 kg sản phẩm loại II;
B. 40 kg sản phẩm loại I và 20 kg sản phẩm loại II;
C. 10 kg sản phẩm loại I và 40 kg sản phẩm loại II;
D. 20 kg sản phẩm loại I và 20 kg sản phẩm loại II.
Lời giải
Đáp án đúng là: A
Gọi x (x ≥ 0 (1)) là số kg loại I cần sản xuất, y (y ≥ 0 (2)) là số kg loại II cần sản xuất.
Số nguyên liệu cần dùng để sản xuất x sản phẩm loại I là: 2x
Số nguyên liệu cần dùng để sản xuất y sản phẩm loại II là: 4y
Xưởng có 200 kg nguyên liệu nên ta có: 2x + 4y ≤ 200 ⇔ x + 2y ≤ 100 ⇔ x + 2y – 100 ≤ 0 (3)
Thời gian để sản xuất x sản phẩm loại I là: 30x
Thời gian để sản xuất y sản phẩm loại II là: 15y
Xưởng có 1 200 giờ làm việc nên ta có: 30x + 15y ≤ 1200 hay 2x + y – 80 ≤ 0 (4)
Xét bất phương trình (1) và điểm A(1; 2) có:
Điểm A không nằm trên đường thẳng x = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng có kể bờ x = 0 và chứa điểm A(1; 2).
Xét bất phương trình (2) và điểm B(0; 1) có:
Điểm B không nằm trên đường thẳng y = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng có kể bờ y = 0 và chứa điểm B(0; 1)
Xét bất phương trình (3) và điểm (0; 0) ta có:
Điểm (0; 0) không nằm trên đường thẳng x + 2y – 100 = 0 và 0 + 2.0 – 100 = –100 < 0 nên miền nghiệm của bất phương trình (3) là nửa mặt phẳng có kể bờ x + 2y – 100 = 0 và chứa điểm (0; 0).
Xét bất phương trình (4) và điểm (0; 0) ta có:
Điểm (0; 0) không nằm trên đường thẳng 2x + y – 80 = 0 và 2.0 + 0 – 80 = –80 < 0 nên miền nghiệm của bất phương trình (4) là nửa mặt phẳng có kể bờ 2x + y – 80 = 0 và chứa điểm (0; 0)
Kết hợp miền nghiệm của các bất phương trình (1), (2), (3) và (4) là miền nghiệm thỏa mãn màu trắng trong hình vẽ:
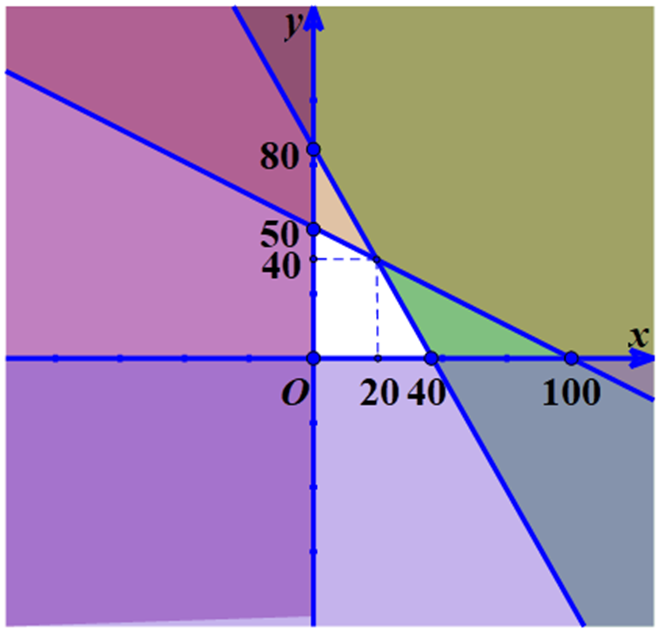
Lợi nhuận thu lại từ x sản phẩm loại I là: 40 000x
Lợi nhuận thu lại từ y sản phẩm loại II là: 30 000y
Tổng lợi nhuận là: 40 000x + 30 000y
Giá trị lớn nhất của L(x; y) = 40 000x + 30 000y đạt tại một trong các điểm (0; 0), (40; 0), (0; 50), (20; 40).
Ta có:
L(0; 0) = 0
L(40; 0) = 1 600 000
L(0; 50) = 1 500 000
L(20; 40) = 2 000 000
Vậy giá trị lớn nhất của L(x; y) là 2 000 000 khi (x; y) = (20; 40).
Vậy cần sản xuất 20kg sản phẩm loại I và 40kg sản phẩm loại II để có mức lợi nhuận lớn nhất
Câu 2
A. 5 lít nước cam và 6 lít nước táo;
B. 4 lít nước cam và 5 lít nước táo;
C. 3 lít nước cam và 6 lít nước táo;
D. 5 lít nước cam và 4 lít nước táo.
Lời giải
Đáp án đúng là: B
Gọi x, y lần lượt là số lít nước cam và táo của một đội pha chế (x, y ≥ 0).
Số điểm thưởng của đội chơi này là: Đ(x; y) = 60x + 80y
Số gam đường cần dùng là 30x + 10y.
Số lít nước cần dùng là x + y.
Số gam hương liệu cần dùng là x + 4y.
Vì trong cuộc thi pha chế, mỗi đội chơi sử dụng tối đa 24g hương liệu, 9 lít nước và 210 g đường nên ta có hệ bất phương trình
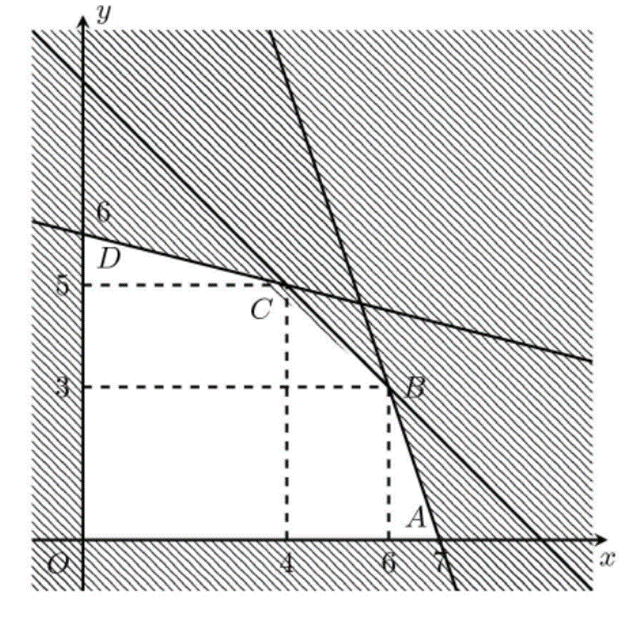
Miền nghiệm của hệ trên là ngũ giác OABCD (kể cả biên). Ta có: Đ(x; y) = 60x + 80y sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ đã cho khi (x; y) là tọa độ của một trong các đỉnh O(0; 0), A(7; 0), B(6; 3), C(4; 5), D(0; 6).
Ta có:
Đ(0; 0) = 60.0 + 80.0 = 0
Đ(7; 0) = 60.7 + 80.0 = 420
Đ(6; 3) = 60.6 + 80.3 = 600
Đ(4; 5) = 60.4 + 80.5 = 640
Đ(0; 6) = 60.0 + 80.6 = 480
Vậy giá trị lớn nhất của D(x; y) là 640 hay để được số điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.
Câu 3
A. 40 cái bánh chưng;
B. 20 cái bánh chưng;
C. 40 cái bánh ống;
D. 20 cái bánh ống.
Lời giải
Đáp án đúng là: A
Gọi số bánh chưng gói được là x, số bánh ống gói được là y. (x, y ≥ 0)
Khi đó số điểm thưởng là F(x; y) = 5x + 7y
Số kg gạo nếp cần dùng là 0,4x + 0,6y
Số kg thịt cần dùng là 0,05x + 0,075y
Số kg đậu xanh cần dùng là 0,1x + 0,15y
Vì trong cuộc thi này chỉ được sử dụng tối đa 20kg gạo nếp, 2kg thịt ba chỉ và 5kg đậu xanh nên ta có hệ bất phương trình
Miền nghiệm của hệ bất phương trình là tam giác OAB (kể cả biên)
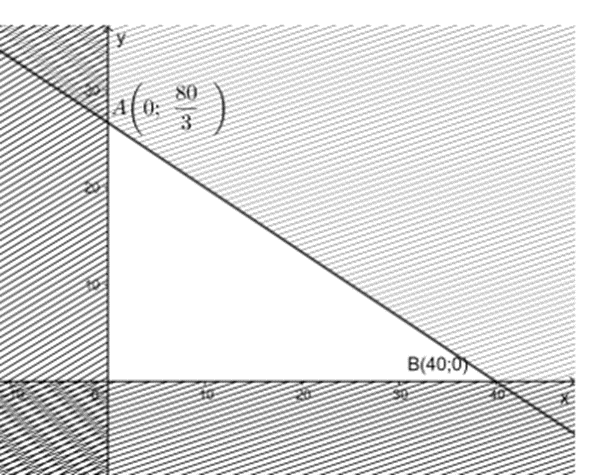
F(x; y) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình trên khi (x; y) là tọa độ một trong các đỉnh O(0; 0), A, B(40; 0) (loại điểm A vì số bánh phải là số nguyên).
Ta có:
F(0; 0) = 5.0 + 7.0 = 0
F(40; 0) = 5.40 + 7.0 = 200
Do đó, F(x; y) lớn nhất là 200. Vậy cần phải gói 40 cái bánh chưng để nhận được số điểm thưởng là lớn nhất.
Câu 4
A. 0,4 kg thịt bò và 0,7 kg thịt lợn;
B. 0,6 kg thịt bò và 1,7 kg thịt lợn;
C. 1,6 kg thịt bò và 2,7 kg thịt lợn;
D. 0,6 kg thịt bò và 0,7 kg thịt lợn.
Lời giải
Đáp án đúng là: D
Gọi x và y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó mua mỗi ngày (0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1)
Khi đó, chi phí để mua số thịt là: F(x; y) = 45x + 35y.
Trong x kg thịt bò có 800x đơn vị protein và 200x đơn vị lipit.
Trong y kg thịt lợn có 600y đơn vị protein và 400y đơn vị lipit.
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên ta có hệ bất phương trình:
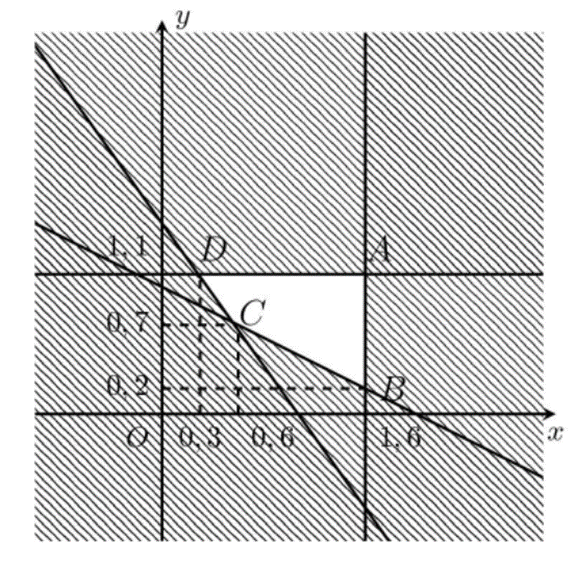
Miền nghiệm của hệ bất phương trình trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên).
Ta có:
F(1,6; 1,1) = 45.1,6 + 35.1,1 = 110,5
F(1,6; 0,2) = 45.1,6 + 35.0,2 = 79
F(0,6; 0,7) = 45.0,6 + 35.0,7 = 51,5
F(0,3; 1,1) = 45.0,3 + 35.1,1 = 52
Vậy F(x; y) nhỏ nhất là 51,5 hay gia đình này cần phải mua 0,6 kg thịt bò và 0,7 kg thịt lợn để số tiền bỏ ra là ít nhất.
Câu 5
A. 5 ha cà phê và 6 ha ca cao;
B. 4 ha cà phê và 6 ha ca cao;
C. 4 ha cà phê và 5 ha ca cao;
D. 10 ha cà phê và 6 ha ca cao.
Lời giải
Đáp án đúng là: B
Gọi x và y lần lượt là số ha cà phê và ca cao mà hộ nông dân này trồng (x ≥ 0, y ≥ 0).
Số tiền cần bỏ ra để thuê người trồng ca cao là 30y.100 000 = 3 000 000y (đồng).
Lợi nhuận thu được là: F(x; y) = 10 000 000x + 12 000 000 – 3 000 000y = 10 000 000x + 9 000 000 y.
Vì số công để trồng cà phê không vượt quá 80 công và gia đình chỉ có 10 ha đất nên ta có hệ phương trình:
Miền nghiệm của hệ trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên). F(x; y) đạt giá trị lớn nhất khi (x; y) là tọa độ của một trong các đỉnh tứ giác.
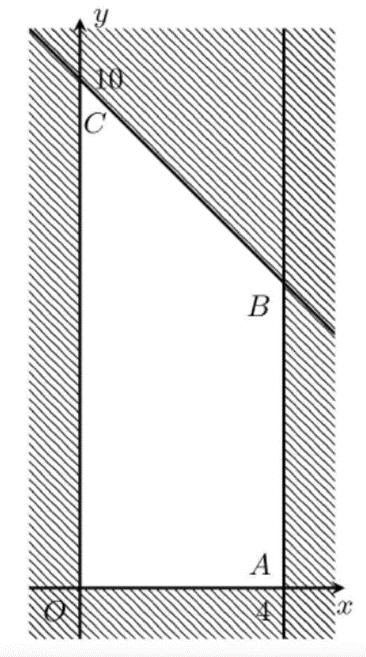
Ta có:
F(0; 0) = 0
F(4; 0) = 40 000 000
F(4; 6) = 94 000 000
F(0; 10) = 90 000 000
Vậy F(x; y) lớn nhất khi (x; y) = (4; 6) hay cần phải trồng 4 ha cà phê và 6 ha ca cao để thu về lợi nhuận lớn nhất.
Câu 6
A. 6 ha đậu và 2 ha cà;
B. 6 ha đậu và 3 ha cà;
C. 4 ha đậu và 2 ha cà;
D. 6 ha đậu và 0 ha cà.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 1 tấn sản phẩm loại A và 3 tấn sản phẩm loại B;
B. 2 tấn sản phẩm loại A và 3 tấn sản phẩm loại B;
C. 4 tấn sản phẩm loại A và 3 tấn sản phẩm loại B;
D. 3 tấn sản phẩm loại A và 3 tấn sản phẩm loại B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 3 xe loại A và 4 xe loại B;
B. 4 xe loại A và 4 xe loại B;
C. 5 xe loại A và 4 xe loại B;
D. 6 xe loại A và 4 xe loại B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 6 ha cà chua và 2 ha cà pháo;
B. 6 ha cà chua và 3 ha cà pháo;
C. 4 ha cà chua và 3 ha cà pháo;
D. 6 ha cà chua và 0 ha cà pháo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 10 mét vuông nuôi lớn, 2 mét vuông nuôi gà;
B. 5 mét vuông nuôi lớn, 0 mét vuông nuôi gà;
C. 8 mét vuông nuôi lớn, 2 mét vuông nuôi gà;
D. 4 mét vuông nuôi lớn, 2 mét vuông nuôi gà.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.