Giải SBT Toán 7 KNTT Bài 31. Quan hệ giữa góc và cạnh đối diện trong một tam giác có đáp án
33 người thi tuần này 4.6 1.5 K lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
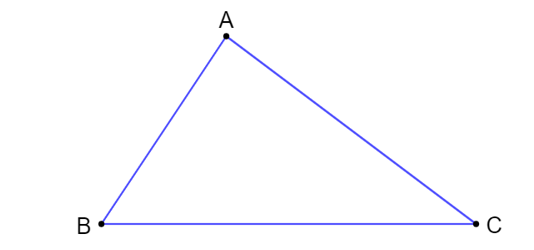
Xét tam giác ABC có BC là cạnh dài nhất và góc đối diện của cạnh BC là nên theo định lí 1 ta có là góc lớn nhất thỏa mãn:
.
Suy ra
Hay
Do đó
Mà tổng ba góc trong một tam giác là 180º.
Nên
Từ đó ta có:
Vậy suy ra số đo góc A lớn hơn hoặc bằng 60º (đpcm).
Lời giải
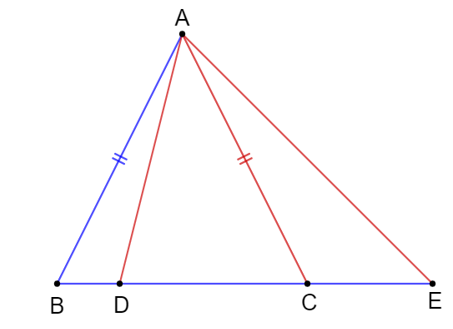
Do trong một tam giác cân, hai góc của đáy luôn bé hơn 90º nên suy ra là góc nhọn.
Mà kề bù với nên suy ra là góc tù.
Xét tam giác ACE có là góc tù nên cạnh đối diện với là cạnh AE là cạnh lớn nhất.
Suy ra AE > AC (*)
Mà tam giác ABC cân tại A nên AB = AC và .
Lại có:
Xét tam giác ABC có:
Suy ra (1)
Xét tam giác ABD có:
Suy ra (2)
Mà D nằm giữa B và C nên suy ra (3)
Từ (1), (2) và (3) ta suy ra:
Hay
Do đó
Áp dụng định lí 2 ta được AB > AD
Mà AB = AC (cmt) nên suy ra AC > AD (**)
Từ (*) và (**) nên suy ra AE > AC > AD (đpcm).
Lời giải
Gọi tam giác ABC vuông tại A và tam giác MNP là tam giác tù tại đỉnh M.
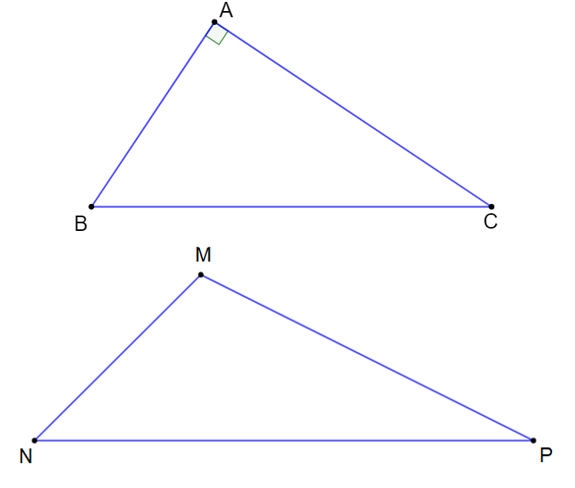
+) Giả sử tam giác ABC là tam giác vuông tại đỉnh A nên suy ra (1)
Lại có tam giác ABC có tổng ba góc trong tam giác bằng 180º nên suy ra:
Hay
Vậy suy ra
Hay ta suy ra được và (2)
Từ (1) và (2) ta có:
Theo định lí 2 ta có BC > AC và BC > AB nên BC là cạnh lớn nhất
Vậy trong tam giác vuông, cạnh huyền là cạnh lớn nhất (đpcm).
+) Giả sử tam giác MNP là tam giác tù tại đỉnh M nên suy ra (3)
Lại có tam giác MNP có tổng ba góc trong tam giác bằng 180º nên suy ra:
Hay
Suy ra
Do đó
Hay ta suy ra được (4)
Từ (3) và (4) ta có:
Theo định lí 2 ta có NP > MP và NP > MN nên NP là cạnh lớn nhất.
Vậy trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất (đpcm).
Lời giải
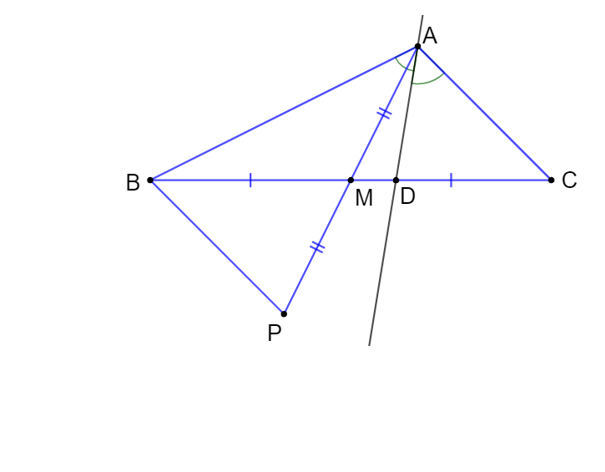
a) Lấy P là điểm thuộc đường thẳng AM sao cho M là trung điểm của AP.
Xét hai tam giác ∆ AMC và ∆ PMB có:
AM = PM (M là trung điểm của AP)
MC = MB (M là trung điểm của BC)
(hai góc đối đỉnh)
Do đó ∆AMC = ∆PMB (c.g.c)
Suy ra (hai góc tương ứng) (1)
Và AC = PB
Mà AB > AC (gt)
Nên suy ra AB > PB
Xét tam giác ABP có AB > PB (cmt) nên theo định lí 1 ta có (2)
Từ (1) và (2) suy ra (3).
Lời giải
b) AD là đường phân giác của góc BAC nên ta có: (4)
Từ (3) và (4) nên suy ra được:
Hay
Suy ra
Do đó MC > DC.
Vậy D là điểm thuộc đoạn thẳng MC.