Giải SBT Toán 7 KNTT Ôn tập chương 9 có đáp án

+) Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất. Nên suy ra phương án A là đúng.

+) Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn.

Suy ra góc nhỏ nhất lớn hơn hoặc bằng 90º.

Hay cả ba góc lớn hơn hoặc bằng 90º.

Suy ra tổng ba góc trong tam giác lớn hơn hoặc bằng: 90º . 3 = 270º.

Điều này vô lý vì tổng ba góc trong tam giác bằng 180º.

Do đó góc đối diện với cạnh nhỏ nhất là góc nhọn.

Nên suy ra đáp án B là đúng.

+) Trong một tam giác, góc đối diện với cạnh lớn nhất luôn là một góc có số đo lớn hơn hoặc bằng 60º (Chứng minh ở bài 9.1 trang 48) nên suy ra nó không chắc chắn là một góc tù. Vậy suy ra đá án C là sai.

+) Trong một tam giác, cạnh đối diện với cạnh lớn nhất là góc tù. Nên suy ra phương án D là đúng.

Chọn đáp án C.

+) Xét bộ ba số: 7, 5, 7 có: 7 – 7 = 0 < 5 và 5 + 7 = 12 > 7.

Do đó ba số 7, 5, 7 là độ dài ba cạnh của một tam giác.

+) Xét bộ ba số: 7, 7, 7 có: 7 – 7 = 0 < 7 và 7 + 7 = 14 > 7.

Do đó ba số 7, 7, 7 là độ dài ba cạnh của một tam giác.

+) Xét bộ ba số: 3, 5, 4 có: 5 – 4 = 1 < 3 và 3 + 4 = 7 > 5

Do đó ba số 3, 5, 4 là độ dài ba cạnh của một tam giác.

+) Xét bộ ba số: 4, 7, 3 có: 3 = 7 − 4 và 7 = 4 + 3

Do đó ba số 4, 7, 3 không là độ dài ba cạnh của một tam giác.

Chọn đáp án D.

Tam giác cân có độ dài cạnh bên b; độ dài cạnh đáy d thì ta phải có: Theo bất đẳng thức trong tam giác suy ra b + b > d.

Hay 2b > d.

Vậy suy ra d < 2b.

Chọn đáp án D.

Áp dụng bất đẳng thức trong tam giác ta có a < b + c nên suy ra

a + a < a + b + c

Hay 2a < a + b + c.

Vậy suy ra $a<\frac{a+b+c}{2}$.

Vậy với mọi tam giác ta đều có: mỗi cạnh nhỏ hơn nửa chu vi.

Chọn đáp án C.

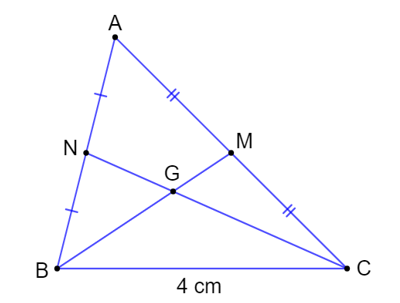
Lấy G là giao điểm của 2 đường trung tuyên BM và CN. Dễ dàng chứng minh được G là trong tâm của tam giác ABC.

Xét tam giác GBC, theo bất đẳng thức tam giác ta có: GB + GC > BC

Mà G là trong tâm tam giác ABC nên ta có:$BG=\frac{2}{3}BM;CG=\frac{2}{3}$ .

Suy ra $\frac{2}{3}\left(BM+CN\right)>BC$

Do đó $BM+CN>\frac{3}{2}BC=\frac{3}{2}.4=6\left(cm\right)$

Vậy tổng độ dài BM + CN có thể là 6,5 cm.

Chọn đáp án D.