Giải VTH Toán 7 Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án
50 người thi tuần này 4.6 1.8 K lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
Đáp án đúng là A
Cho tam giác ABC, ta có:
Góc A kề cạnh AB và AC, góc C kề cạnh AC và BC. Do đó phát biểu A đúng và C sai.
Góc A xen giũa cạnh AB và AC. Do đó B sai.
Góc B và C kề cạnh BC. Do đó D sai.
Lời giải
Đáp án đúng là C
+) Ta có: tam giác ABC bằng tam giác MNP nên: BC = NP, , (các cặp cạnh và cặp góc tương ứng).
+) Các yếu tố trong các đáp án liên quan đến hai cặp góc và một cặp cạnh nên trường hợp được dùng để chứng minh hai tam giác ABC và MNP là góc – cạnh – góc. Do đó nếu BC = NP, , thì hai tam giác ABC và MNP bằng nhau.
Vậy hai tam giác ABC và MNP bằng nhau khi và chỉ khi BC = NP,,
Lời giải
+) Ta có: tam giác ABC bằng tam giác MNP nên: AB = MN, AC = MP và (các cặp cạnh và cặp góc tương ứng).
+) Các yếu tố trong các đáp án liên quan đến một cặp góc và hai cặp cạnh nên trường hợp được dùng để chứng minh hai tam giác ABC và MNP là góc – cạnh – góc. Do đó nếu AB = MN, AC = MP và thì hai tam giác ABC và MNP bằng nhau.
Vậy hai tam giác ABC và MNP bằng nhau khi và chỉ khi AB = MN, AC = MP và .
Lời giải
Theo hình vẽ, ta có:
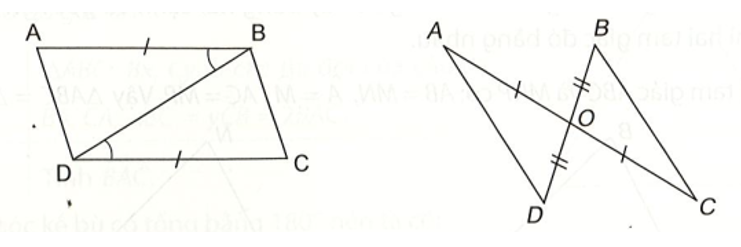
∆ABD = ∆CDB (c – g – c) vì: AB = CD, (theo giả thiết), BD là cạnh chung.
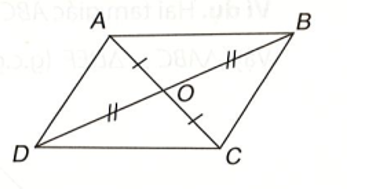
∆AOD = ∆COB (c – g – c), vì OA = OC (theo giả thiết), (2 góc đối đỉnh), OD = OB (theo giả thiết).
Lời giải
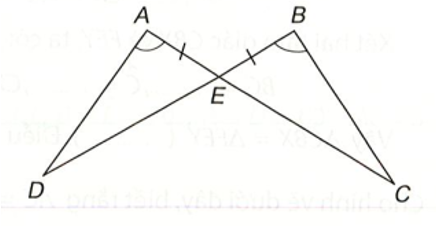
a) Theo hình vẽ bên ta có: ∆AOD = ∆COB (c – g – c), vì:
OA = OC (theo giả thiết), (2 góc đối đỉnh), OD = OB (theo giả thiết).
∆AOB = ∆COD (c – g – c), vì:
OA = OC (theo giả thiết), (2 góc đối đỉnh), OB = OD (theo giả thiết).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.