20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 4. Hai mặt phẳng song song (Đúng sai - Trả lời ngắn) có đáp án

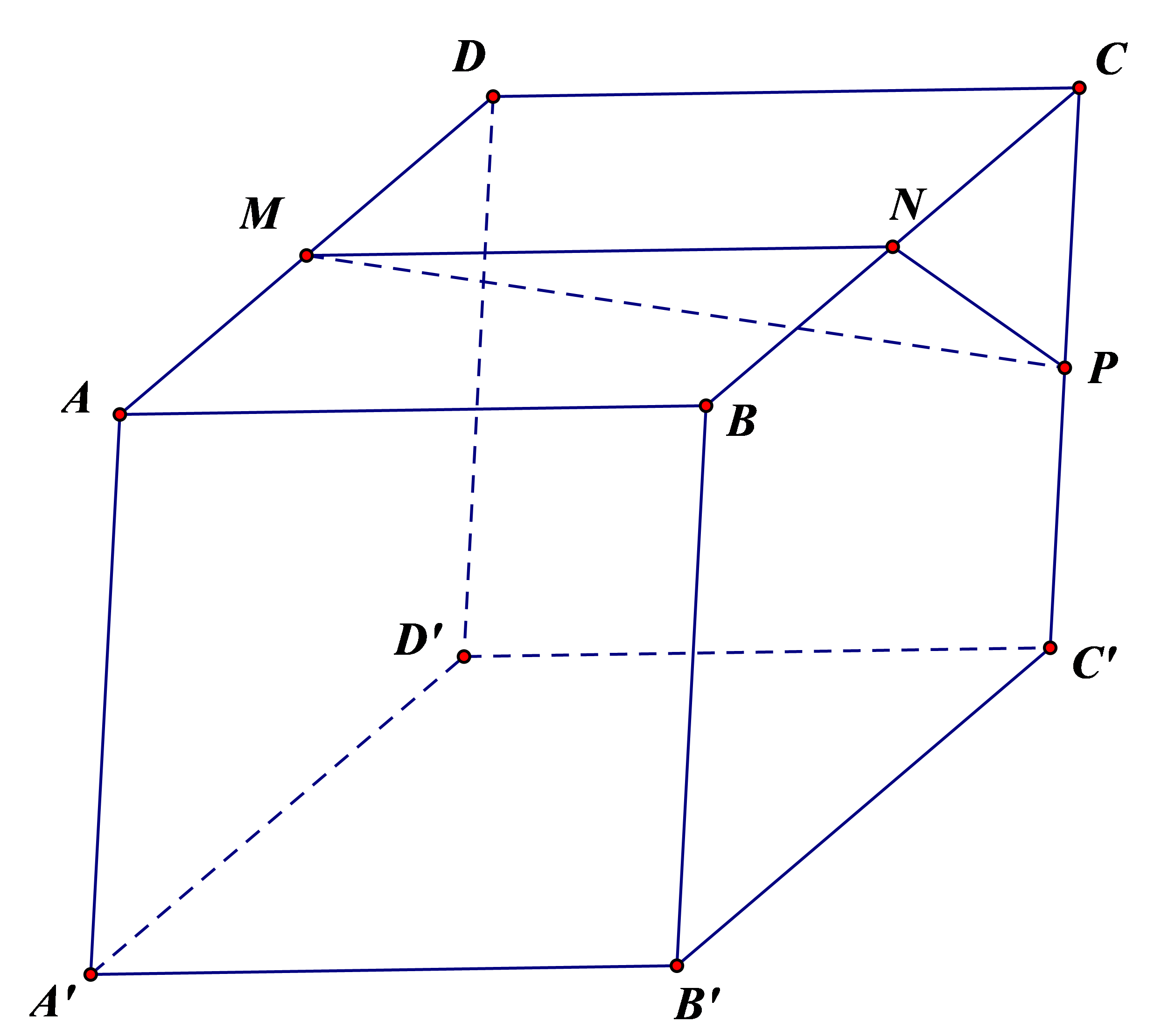
+ Trong không gian, hai mặt phẳng có \(3\) vị trí tương đối: trùng nhau, cắt nhau, song song với nhau. Vì vậy, \(2\) mặt phẳng không cắt nhau thì có thể song song hoặc trùng nhau \( \Rightarrow \)A là mệnh đề sai.

+ Hai mặt phẳng cùng song song với một đường thẳng thì chúng có thể song song với nhau (hình vẽ) \( \Rightarrow \) B là mệnh đề sai.

+Ta có:\[a\parallel \left( P \right),a\parallel \left( Q \right)\] nhưng \(\left( P \right)\) và \(\left( Q \right)\) vẫn có thể song song với nhau.

Mệnh đề C là tính chất  nên C đúng.

\(\left( \alpha  \right)\parallel a\) và \(\left( \alpha  \right)\parallel b\) với \(a,b\) là hai đường thẳng cắt nhau thuộc\(\left( \beta  \right)\) thì (α) // (β).

Nếu \(a\) cắt \(b\) và \(a\parallel a',\;b\parallel b'\) thì \(\left( \alpha  \right)\parallel \left( \beta  \right).\)

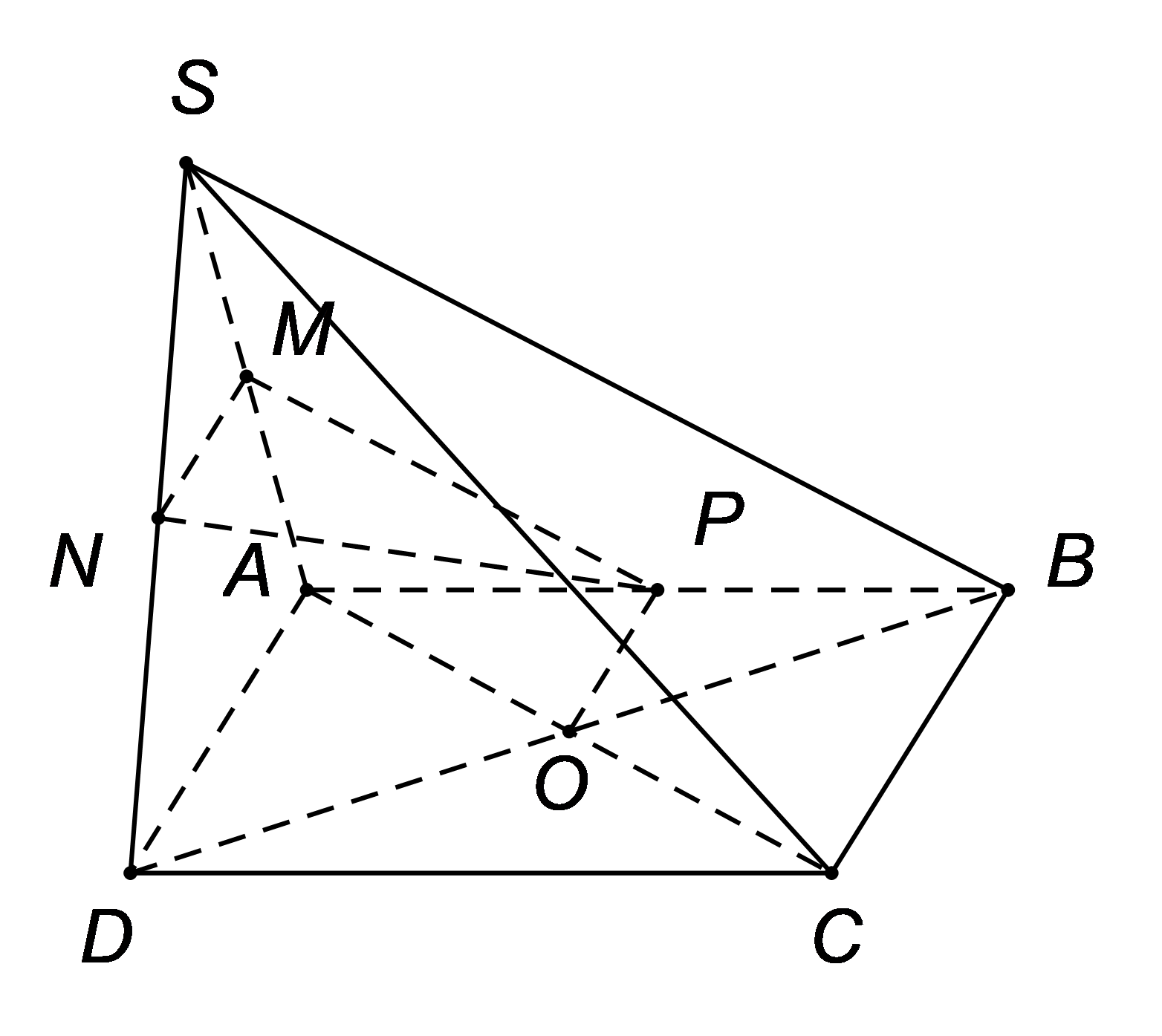
Ta có \[MN\] là đường trung bình của tam giác \[SAD\] suy ra \[MN\]//\[AD.\]   \[\,\left( 1 \right)\]

Và \[OP\] là đường trung bình của tam giác \[BAD\] suy ra \[OP\]//\[AD.\]   \[\,\left( 2 \right)\]

Từ \[\left( 1 \right),\left( 2 \right)\] suy ra \[MN\]//\[OP\]//\[AD\] \[ \Rightarrow \,\,M,\,\,N,\,\,O,\,\,P\] đồng phẳng.

Lại có \[MP\]//\[SB,\,\,\,OP\]//\[BC\] suy ra \[\left( {MNOP} \right)\]//\[\left( {SBC} \right)\] hay \[\left( {MON} \right)\]//\[\left( {SBC} \right).\]

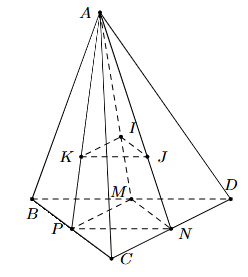
Ta có \(\frac{{AK}}{{AP}} = \frac{{AI}}{{AM}} = \frac{{AJ}}{{AN}} = \frac{2}{3}\) nên KJ // PN Þ KJ // (BCD) và IJ // MN Þ IJ // (BCD).

Mà KJ, IJ Ì (KIJ) và  KJ Ç IJ = J nên (KIJ) // (BCD).

Vì I, J lần lượt là trung điểm của SB và AB nên IJ // SA.

Do J là trung điểm AB và AB = 2CD nên AJ = CD.

Mà AJ // CD nên AJCD là hình bình hành.

Do đó CJ // AD.

Ta có \(\left\{ \begin{array}{l}IJ//SA\\JC//AD\\IJ,JC \subset \left( {CIJ} \right)\\SA,AD \subset \left( {SAD} \right)\\CJ \cap IJ = J\end{array} \right. \Rightarrow \left( {CIJ} \right)//\left( {SAD} \right)\).

Các mặt bên của hình lăng trụ là các hình hình hành, chúng bằng nhau nếu hình lăng trụ có đáy là đa giác đều.

Dựa vào hình vẽ và tính chất của hình hộp chữ nhật, ta thấy rằng:

Hình hộp có đáy \[ABCD\] là hình bình hành.

Các đường thẳng \[{A_1}C,\,\,A{C_1},\,\,D{B_1},\,\,{D_1}B\] cắt nhau tại tâm của \[A{A_1}{C_1}C,\,\,\,BD{D_1}{B_1}.\]

Hai mặt bên \(\left( {AD{D_1}{A_1}} \right),\,\,\left( {BC{C_1}{B_1}} \right)\) đối diện và song song với nhau.

\[A{D_1}\] và \[CB\] là hai đường thẳng chéo nhau suy ra \[A{D_1}CB\] không phải là hình chữ nhật.