Đề kiểm tra Đường tiệm cận của đồ thị hàm số (có lời giải) - Đề 5
46 người thi tuần này 4.6 0.9 K lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
PHẦN I: Câu trắc nghiệm nhiều phương án lựa chonl. Thí sinh trả lời từ câu 1 đến câu 12 Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f(x)\) có \[\mathop {\lim }\limits_{x \to + \infty } f(x) = 3\] và \[\mathop {\lim }\limits_{x \to - \infty } f(x) = - 3\]. Khẳng định nào sau đây là khẳng định đúng?
Lời giải
Dựa vào định nghĩa đường tiệm cận ngang của đồ thị hàm số ta chọn đáp án D.
Câu 2
Lời giải
Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{{16}}{5}} \right\}\). Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{x - 3}}{{5x - 16}} = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{1 - \frac{3}{x}}}{{5 - \frac{{16}}{x}}} = \frac{1}{5}\).
Vậy đường thẳng\(y = \frac{1}{5}\) là tiệm cận ngang của đồ thị hàm số đã cho.
Câu 3
Lời giải
Chọn C.
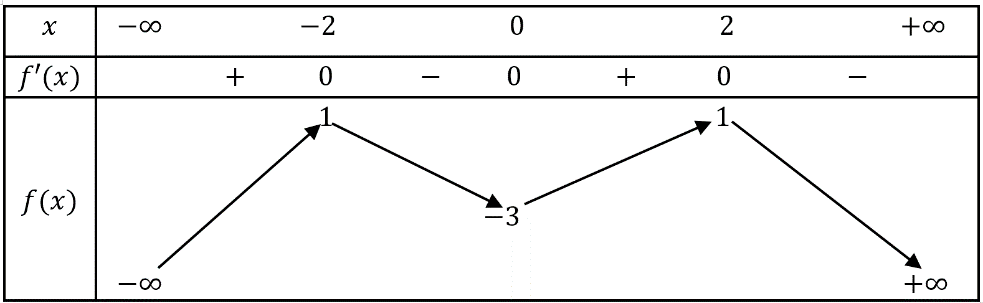
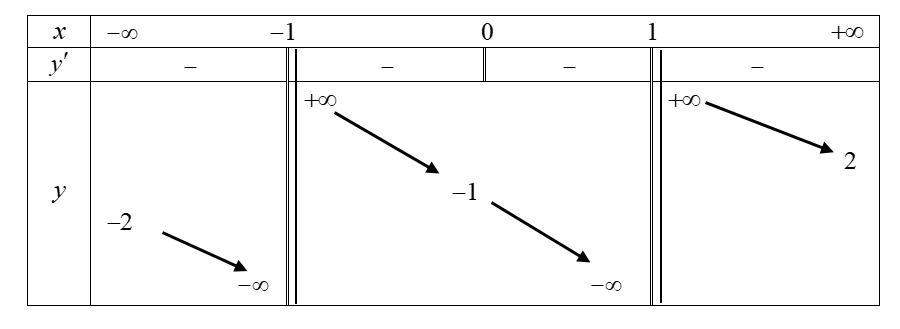
Lời giải
Chọn C vì nhìn bảng biến thiên thấy ngay đồ thị có tiệm cận ngang \(y = - 2\) và \(y = 2\).
Câu 5
Lời giải
Dựa vào định nghĩa đường tiệm cận đứng của đồ thị hàm số ta chọn đáp án A.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
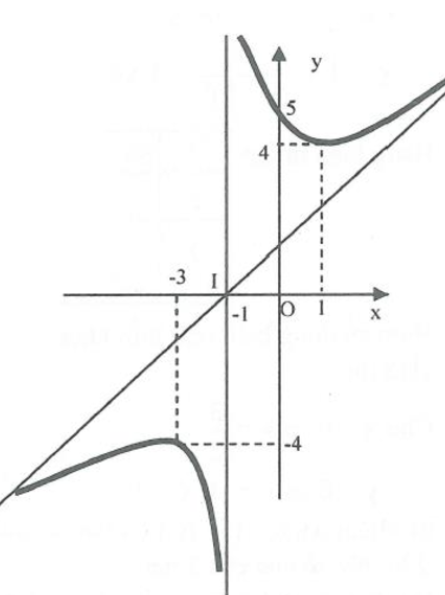
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình vẽ.
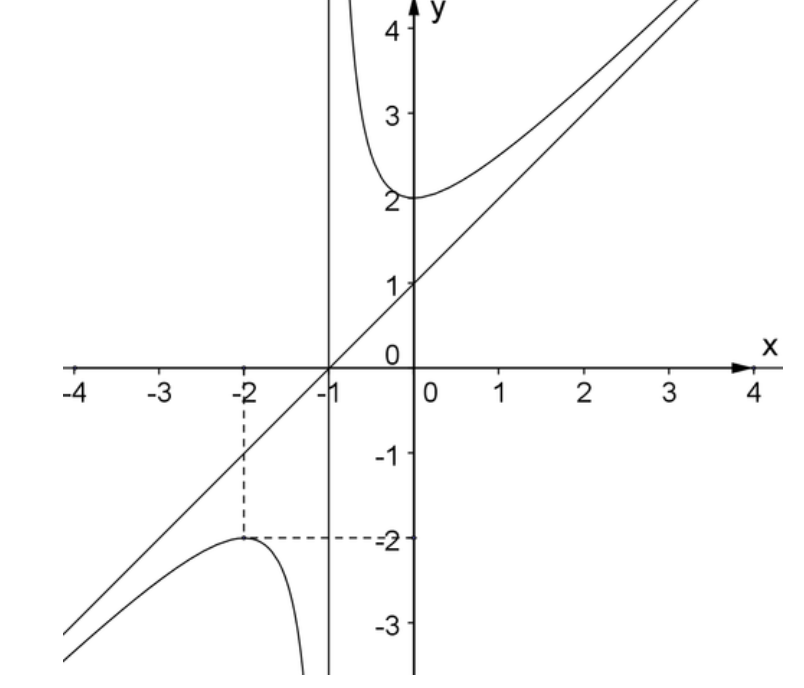
Tiệm cận xiên của đồ thị hàm số đã cho là

Tiệm cận xiên của đồ thị hàm số đã cho là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
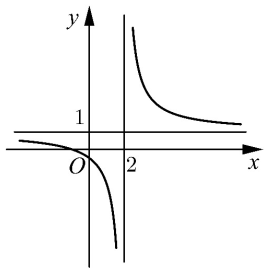
Cho hàm số \(y = \frac{{x + 2}}{{x - 2}}\) có đồ thị là \(\left( C \right)\).
a) [NB]. Đồ thị \(\left( C \right)\) có đường tiệm cận đứng \(x = 2\).
b) [TH]. Đồ thị \(\left( C \right)\) nhận điểm \(I\left( {1;1} \right)\) làm tâm đối xứng.
c) [VD]. Đường thẳng đường thẳng \(d:y = x - 1\) cắt đồ thị \(\left( C \right)\) tại \(2\) điểm phân biệt có độ dài bằng \(4\sqrt 5 .\)
d) [VDC]. Gọi \(M\) là điểm bất kì thuộc đồ thị \(\left( C \right)\). Khi đó tổng khoảng cách từ điểm \(M\) đến hai đường tiệm cận của đồ thị \(\left( C \right)\) đạt giá trị nhỏ nhất bằng \(4.\)
Cho hàm số \(y = \frac{{x + 2}}{{x - 2}}\) có đồ thị là \(\left( C \right)\).
a) [NB]. Đồ thị \(\left( C \right)\) có đường tiệm cận đứng \(x = 2\).
b) [TH]. Đồ thị \(\left( C \right)\) nhận điểm \(I\left( {1;1} \right)\) làm tâm đối xứng.
c) [VD]. Đường thẳng đường thẳng \(d:y = x - 1\) cắt đồ thị \(\left( C \right)\) tại \(2\) điểm phân biệt có độ dài bằng \(4\sqrt 5 .\)
d) [VDC]. Gọi \(M\) là điểm bất kì thuộc đồ thị \(\left( C \right)\). Khi đó tổng khoảng cách từ điểm \(M\) đến hai đường tiệm cận của đồ thị \(\left( C \right)\) đạt giá trị nhỏ nhất bằng \(4.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Đặt \[h\left( x \right) = g\left( {\frac{{{x^2} - 6x + 5}}{{{x^2} + 6x + 5}}} \right)\]. Khi đó hàm số \[y = h\left( x \right)\] có \(5\) điểm cực trị. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759196717.png)